题目内容
6.解下列二元一次方程组:(1)$\left\{\begin{array}{l}{2(x+y-1)=3(3-y)-3}\\{\frac{x}{3}+\frac{y}{2}=2}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{2x-3y}{6}=4}\\{\frac{(5x+15y)-5}{3}=0}\end{array}\right.$.
分析 (1)、(2)分别把各方程组中的方程化为不含分母及括号的方程,再用代入消元法和加减消元法求解即可.
解答 解:(1)原方程组可化为$\left\{\begin{array}{l}{2x+5y=8①}\\{2x+3y=12②}\end{array}\right.$,
①-②得,2y=-4,解得y=-2,把y=-2代入①得,2x-10=8,解得x=9,
故原方程组的解为$\left\{\begin{array}{l}{x=9}\\{y=-2}\end{array}\right.$;
(2)原方程组可化为$\left\{\begin{array}{l}{2x-3y=8①}\\{x+3y=1②}\end{array}\right.$,
①+②得,3x=9,解得x=3,把x=3代入②得,3+3y=1,解得y=-$\frac{2}{3}$.
故原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-\frac{2}{3}}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
相关题目
16.符号[x]表示不超过x的最大整数,例如[2.6]=2,[-1]=-1,[-2.6]=-3.若关于x的方程[x]+[3x]=kx(k≠0)在0<x<1内有解,则k的取值范围是( )
| A. | $\frac{3}{2}$<k≤3 | B. | 2<k≤3 | C. | 2≤k≤3 | D. | $\frac{3}{2}$<k≤2 |
1.计算sin45°的值等于( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
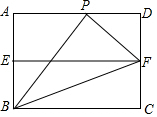 如图,在矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点,P是AD上一点,∠PFB=3∠FBC,则线段PD的长度$\frac{4}{3}$.
如图,在矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点,P是AD上一点,∠PFB=3∠FBC,则线段PD的长度$\frac{4}{3}$.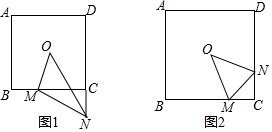
 已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,AB=4cm,求CM和AD的长.
已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,AB=4cm,求CM和AD的长. 如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.
如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.