题目内容
9．在Rt△ABC中，∠C=90°，AB=5，BC=3，则AC为（ ）| A． | 4 | B． | 16 | C． | $\sqrt{34}$ | D． | 8 |
分析 根据勾股定理进行计算即可得出结果．
解答 解：∵Rt△ABC中，∠C=90°，AB=5，BC=3，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4；
故选：A．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
如图，在正方形ABCD的对角线BD上取点E，使得∠BAE=75°，连接AE，CE，将线段CE绕点C顺时针旋转，使点E的对应点恰好落在AE延长线上的点F处．若AB=2，则AF的长为$\frac{4\sqrt{6}}{3}$．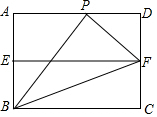
如图，在矩形ABCD中，AB=2，AD=3，E、F分别是AB、CD的中点，P是AD上一点，∠PFB=3∠FBC，则线段PD的长度$\frac{4}{3}$．
1．计算sin45°的值等于（ ）
| A． | $\sqrt{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，AB=4cm，求CM和AD的长．