题目内容
7. 如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F
如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F(1)求证:△BDE∽△ADB;
(2)若AB=2$\sqrt{5}$,AD=4,求CF的长.
分析 (1)由D是弧BC的中点,得到$\widehat{CD}$=$\widehat{BD}$,求得∠BAD=∠DBE,根据相似三角形的判定定理即可得到结论;
(2)由AB是半圆O的直径,得到AD⊥BF,BC⊥AF,根据勾股定理得到BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=2,根据全等三角形的性质得到DF=BD=2,然后由相似三角形的性质即可得到结论.
解答 (1)证明:∵D是弧BC的中点,
∴$\widehat{CD}$=$\widehat{BD}$,
∴∠BAD=∠DBE,
∵∠BDE=∠ADB,
∴△BDE∽△ADB;
(2)解:∵AB是半圆O的直径,
∴AD⊥BF,BC⊥AF,
∵AB=2$\sqrt{5}$,AD=4,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=2,
在△ABD与△AFD中,$\left\{\begin{array}{l}{∠FAD=∠BAD}\\{AD=AD}\\{∠ADF=∠ADB=90°}\end{array}\right.$,
∴△ABD≌△AFD,
∴DF=BD=2,
∴BF=4,
∵∠BCF=∠ADB=90°,
∴△ABD∽△BFC,
∴$\frac{AB}{BF}=\frac{BD}{CF}$,即$\frac{2\sqrt{5}}{4}$=$\frac{2}{CF}$,
∴CF=$\frac{4\sqrt{5}}{5}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,勾股定理,圆周角定理,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.下列各点中,在直线y=2x-3上的是( )
| A. | (0,3) | B. | (1,1) | C. | (2,1) | D. | (-1,5) |
2.下列事件中属于必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | B. | 367人中至少有2人的生日相同 | ||
| C. | 掷一次骰子,向上的一面是6点 | D. | 某射击运动员射击1次,命中靶心 |
12.在实数-$\sqrt{2}$,-$\frac{1}{3}$,0,π,4中,无理数的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.符号[x]表示不超过x的最大整数,例如[2.6]=2,[-1]=-1,[-2.6]=-3.若关于x的方程[x]+[3x]=kx(k≠0)在0<x<1内有解,则k的取值范围是( )
| A. | $\frac{3}{2}$<k≤3 | B. | 2<k≤3 | C. | 2≤k≤3 | D. | $\frac{3}{2}$<k≤2 |
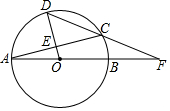 如图,AB是⊙O的直径,D是$\widehat{AC}$上一点,且OD经过AC的中点E,连接DC并延长交AB的延长线于点F.
如图,AB是⊙O的直径,D是$\widehat{AC}$上一点,且OD经过AC的中点E,连接DC并延长交AB的延长线于点F. 如图,在正方形ABCD的对角线BD上取点E,使得∠BAE=75°,连接AE,CE,将线段CE绕点C顺时针旋转,使点E的对应点恰好落在AE延长线上的点F处.若AB=2,则AF的长为$\frac{4\sqrt{6}}{3}$.
如图,在正方形ABCD的对角线BD上取点E,使得∠BAE=75°,连接AE,CE,将线段CE绕点C顺时针旋转,使点E的对应点恰好落在AE延长线上的点F处.若AB=2,则AF的长为$\frac{4\sqrt{6}}{3}$.