题目内容
2.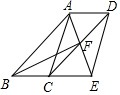 四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.(1)求证:BE=CD;
(2)连接BF、AC、DE,当BF⊥AE时,求证:四边形ACED是平行四边形.
分析 (1)只要证明AB=CD,AB=BE即可解决问题.
(2)只要证明△DAF≌△CEF推出AD=CE,即可解决问题.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∵AE平分∠BAD,
∴∠EAB=∠EAD=∠AEB,
∴AB=BE,
∴BE=CD.
(2)∵BA=BE,BF⊥AE,
∴AF=EF,
∵AD∥CE,
∴∠DAF=∠CEF,
在△ADF和△ECF中,
$\left\{\begin{array}{l}{∠DAF=∠CEF}\\{AF=FE}\\{∠AFD=∠CFE}\end{array}\right.$,
∴△DAF≌△CEF
∴AD=CE,∵AD∥CE,
∴四边形ADEC是平行四边形.
点评 本题考查平行四边形的性质、角平分线的定义、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2. 如图,在△ABC中,AB=AC,AD∥BC,若∠BAD=110°,则∠BCA的大小为( )
如图,在△ABC中,AB=AC,AD∥BC,若∠BAD=110°,则∠BCA的大小为( )
 如图,在△ABC中,AB=AC,AD∥BC,若∠BAD=110°,则∠BCA的大小为( )
如图,在△ABC中,AB=AC,AD∥BC,若∠BAD=110°,则∠BCA的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
14.下列计算正确的是( )
| A. | (x-2)2=x2-4 | B. | (m+n)2=m2+n2 | C. | (x+2)(x-2)=x2-4 | D. | (m-n)2=m2-2mn-n2 |
12. 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
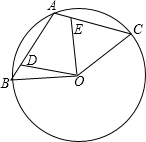 已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE. 画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.
画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.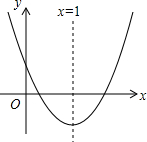 如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③$\frac{b}{c}$<-2;④an2+bn=a(2-n)2+b(2-n)(n为任意实数),其中正确的结论个数是( )
如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③$\frac{b}{c}$<-2;④an2+bn=a(2-n)2+b(2-n)(n为任意实数),其中正确的结论个数是( )