题目内容
12. 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
分析 根据平行线的性质得到∠3=∠1=125°,由平角的定义得到∠4=180°-∠3=55°,由余角的定义即可得到结论.
解答  解:∵AB∥CD,
解:∵AB∥CD,
∴∠3=∠1=125°,
∴∠4=180°-∠3=55°,
∵CD⊥EF,
∴∠CEF=90°,
∴∠2=35°,
故选B.
点评 本题考查了平行线的性质,垂线的定义,熟练掌握平行线的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.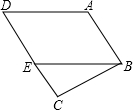 如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
解:∵AB∥CD (已知)
∴∠ABE=∠BEC(两直线平行,内错角相等)
∵AD∥BE (已知)
∴∠D=∠BCE
∴∠ABE=∠D ( 等量代换)
 如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.解:∵AB∥CD (已知)
∴∠ABE=∠BEC(两直线平行,内错角相等)
∵AD∥BE (已知)
∴∠D=∠BCE
∴∠ABE=∠D ( 等量代换)
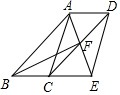 四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.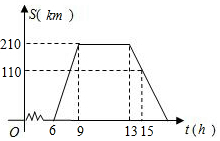 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: 如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )