题目内容
13.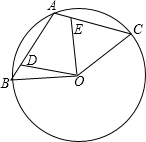 已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.求证:OD=OE.
分析 连接OA,由于A是弧BC的中点,所以AB=AC,然后证明△OBD≌△OAE即可求证OD=OE
解答 解:连接OA,
∵点A是弧BC的中点,
∴AB=AC,∠BOA=∠AOC,
∵OA=OB=OC,
∴∠B=∠OAC
∵AD=CE,
∴BD=AE,
在△OBD与△OAE中,
$\left\{\begin{array}{l}{OB=OA}\\{∠B=∠OAC}\\{BD=AE}\end{array}\right.$,
∴△OBD≌△OAE(SAS)
∴OD=OE
点评 本题考查圆的性质,解题的关键是证明△OBD≌△OAE,本题属于基础题型.

练习册系列答案
相关题目
8.已知在△ABC中,AB=14,BC=13,tanB=$\frac{12}{5}$,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{25}$ | D. | $\frac{56}{65}$ |


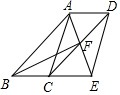 四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.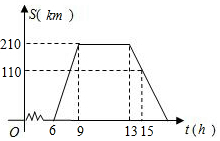 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: