题目内容
9．若A（x1，y1），B（x2，y2）为一次函数y=3x-1图象上的两个不同的点，且x1x2≠0，x1＜x2，设$M=\frac{{1+{y_1}}}{x_1}，N=\frac{{1+{y_2}}}{x_2}$，则（ ）| A． | M＞N | B． | M=N | C． | M＜N | D． | 无法确定 |
分析 首先由一次函数图象上点的坐标特征可以求得M、N的值，然后来比较它们的大小即可．
解答 解：∵一次函数的解析式是y=3x-1，
∴$\frac{1+y}{x}$=3（x≠0）；
又∵A（x1，y1），B（x2，y2）为一次函数y=3x-1的图象上的两个不同的点，设$M=\frac{{1+{y_1}}}{x_1}，N=\frac{{1+{y_2}}}{x_2}$，
∴M=$\frac{1+{y}_{1}}{{x}_{1}}$=3，N=$\frac{1+{y}_{2}}{{x}_{2}}$=3，
∴M=N，
故选B．
点评 本题考查了反比例函数图象上点的坐标特征，经过函数的某点一定在函数的图象上．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，AB是⊙O的直径，AC是弦，D是$\widehat{AC}$的中点，DE⊥AB于E，DF交AC于按F，DB交AC于点G．下面结论：①FA=FD=FG；②FG=GC；③CD是DG与DB的比例中项；④$\frac{EO}{OB}$=$\frac{EF}{FD}$，其中正确的结论有3个．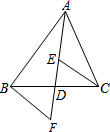
AD是△ABC的中线，DE=DF．下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（ ）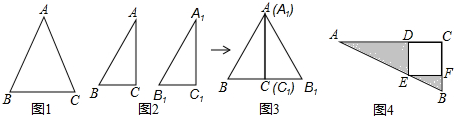
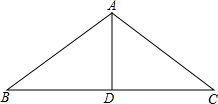如图，已知△ABC中，AB=AC，AD平分∠BAC，求证：BD=CD．