题目内容
19.某商店经营儿童益智玩具,已知成批购进时的单价是20元,调查发现,销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具的售价不能高于40元.设每件玩具的销售单价上涨了x元,(x为整数)月销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)如果商店想要每月获得的利润不低于2520元,那么每月用于购进这种玩具的成本需要多少元?
(4)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
分析 (1)根据利润=数量×每件的利润就可以求出关系式;
(2)当y=2520时代入(1)的解析式就可以求出结论;
(3)画出二次函数的大致图象,由二次函数的性质得出答案即可;
(4)根据(1)的解析式,将其转化为顶点式,根据二次函数的顶点式的性质就可以求出结论.
解答 解:(1)依题意得:
y=(30-20+x)(230-10x)
y=-10x2+130x+2300.
∵每件首饰售价不能高于40元.
∴0≤x≤10.
答:求y与x的函数关系式为:y=-10x2+130x+2300,x的取值范围为0≤x≤10;
(2)当y=2520时,
-10x2+130x+2300=2520
∴x2-13x+22=0,
∴x1=2,x2=11,
∵0≤x≤10,
∴x=2,
∴当x=2时,30+x=32.
答:每件首饰的售价定为32元时月销售利润恰好为2520元;
(3)如图,
由题可知:当每件玩具的销售单价上涨了2、3、4、5、6、7、8、9、10、11元,每月获得的利润不低于2520元,
对应的销售量为210、200、190、180、170、160、150、140、130、120,
每月用于购进这种玩具的成本需要4200元、4000元、3800元、3600元、3400元、3200元、3000元、2800元、2600元、2400元.
(4)∵y=-10x2+130x+2300.
∴y=-10(x-6.5)2+2722.5.
∴a=-10<0.
∴当x=6.5时,y最大=2722.5.
∴每件首饰的售价定为:30+6.5=36.5元.
答:每件首饰的售价定为36.5元时,可使月销售利润最大,最大的月利润是2722.5元.
点评 本题考查了二次函数的解析式的运用,根据解析式的函数值求自变量的值的运用,二次函数的顶点式的性质的运用,解答时求出二次函数的解析式是关键.

| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
(2)若该水果进价为13元/千克,设销售利润为W(元);试求销售利润W(元)与销售价x(元/千克)之间的函数关系式,求当x取何值时,销售利润最大?
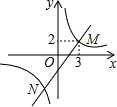 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )| A. | 2,2 | B. | 3,8 | C. | 2,6 | D. | -2,-8 |
| A. |  | B. |  | C. |  | D. |  |
 已知△ABC的三个顶点的坐标分别是A(-4,0),B(2,0),C(-5,4).
已知△ABC的三个顶点的坐标分别是A(-4,0),B(2,0),C(-5,4). 已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,
已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,