题目内容
14.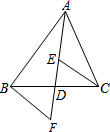 AD是△ABC的中线,DE=DF.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
AD是△ABC的中线,DE=DF.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据三角形中线的定义可得BD=CD,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE,最后根据等底等高的三角形的面积相等判断出②正确.
解答 解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDF=∠CDE}\\{DE=DF}\end{array}\right.$,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BF∥CE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的是①②③④.
故答案为:①②③④.
点评 本题考查了全等三角形的判定与性质,等底等高的三角形的面积相等,熟练掌握三角形全等的判定方法并准确识图是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
9.若A(x1,y1),B(x2,y2)为一次函数y=3x-1图象上的两个不同的点,且x1x2≠0,x1<x2,设$M=\frac{{1+{y_1}}}{x_1},N=\frac{{1+{y_2}}}{x_2}$,则( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
4.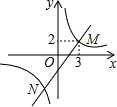 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )| A. | 2,2 | B. | 3,8 | C. | 2,6 | D. | -2,-8 |
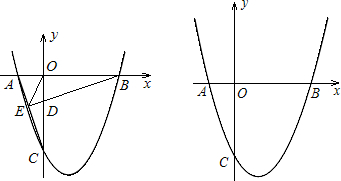
 已知:如图,BE⊥CD,BE=DE,BC=DA.
已知:如图,BE⊥CD,BE=DE,BC=DA.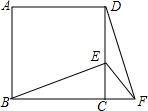 如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.