题目内容
1.阅读理解:“分割、拼凑法”是几何证明中常用的方法.苏科版八上数学第一章《全等三角形》中,有以下两道题,其中问题1中的图1分割成两个全等三角形,而问题2是“HL定理”的证明,却将图2两个直角三角形拼成了一个等腰三角形图3.请按照上面的思路,补全问题1、2的解答:
问题1:已知:如图1,在△ABC中,AB=AC.求证:∠B=∠C.
问题2:如图2,在△ABC和△A1B1C1中,∠C=∠C1=90°,AB=A1B1,AC=A1C1.
求证:△ABC≌△A1B1C1(补全证明过程).
证明:把两个直角三角形如图3所示拼在一起仿照上面的方法解答问题:
问题3:如图4,△ABC中,∠ACB=90°,四边形CDEF是正方形,AE=5,BE=3.求阴影部分的面积和.
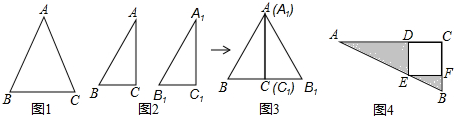
分析 问题1:作中线AD,根据三角形全等的判定定理证明△ABD≌△ACD,根据全等三角形的性质定理证明结论;
问题2:根据直角三角形全等的判定定理即可得到结论;
问题3:把△ADE逆时针旋转90°,则DE和DF重合,此时△A′BD为直角三角形,且A′D=36,BD=4,可求得面积.
解答 问题1: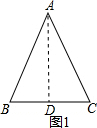 证明:作中线AD,
证明:作中线AD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD,
∴∠B=∠C;
问题2:证明:∵∠C=∠C1=90°,
在Rt△ABC和Rt△A1B1C1中,
$\left\{\begin{array}{l}{AB={A}_{1}{B}_{1}}\\{AC={A}_{1}{C}_{1}}\end{array}\right.$,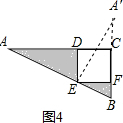
∴Rt△ABC≌△RtA1B1C1;
问题3:解:如图4,把△ADE逆时针旋转90°,
则△ADE≌△A′DF,
∴A′E=AE=5,∠A′EF=∠AED,
∵∠AED+∠BEF=90°,
∴∠A′EF+∠BEF=∠A′EB=90°,
∴S阴影=S△ADE+S△BEF=S△A′FE+S△BEF=S△A′EB=$\frac{1}{2}$A′E•BE=$\frac{1}{2}$×5×3=$\frac{15}{2}$.
点评 本题主要考查全等三角形的判定和性质,等腰三角形的性质,正方形的性质及旋转的性质,利用旋转把阴影部分转化成Rt△A′BD是解题的关键.

练习册系列答案
相关题目
9.若A(x1,y1),B(x2,y2)为一次函数y=3x-1图象上的两个不同的点,且x1x2≠0,x1<x2,设$M=\frac{{1+{y_1}}}{x_1},N=\frac{{1+{y_2}}}{x_2}$,则( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
13.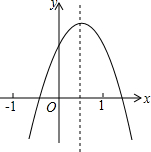 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
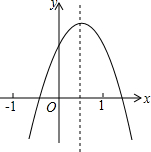 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a-b+c<0 |
 如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD=60°.
如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD=60°. 已知△ABC的三个顶点的坐标分别是A(-4,0),B(2,0),C(-5,4).
已知△ABC的三个顶点的坐标分别是A(-4,0),B(2,0),C(-5,4).