题目内容
1.若一元二次方程ax2=b(ab>0)的两个根分别是m+1与2m-4,则$\frac{b}{a}$=4.分析 利用直接开平方法得到x=±$\sqrt{\frac{b}{a}}$,得到方程的两个根互为相反数,所以m+1+2m-4=0,解得m=1,则方程的两个根分别是2与-2,则有$\sqrt{\frac{b}{a}}$=2,然后两边平方得到$\frac{b}{a}$=4.
解答 解:由题意两根不相等,
∵x2=$\frac{b}{a}$,
∴x=±$\sqrt{\frac{b}{a}}$,
∴方程的两个根互为相反数,
∴m+1+2m-4=0,解得m=1,
∴一元二次方程ax2=b的两个根分别是2与-2,
∴$\sqrt{\frac{b}{a}}$=2,
∴$\frac{b}{a}$=4.
故答案为:4.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.如果方程化成x2=p的形式,那么可得x=±$\sqrt{p}$;如果方程能化成(nx+m)2=p(p≥0)的形式,那么nx+m=±$\sqrt{p}$.

练习册系列答案
相关题目
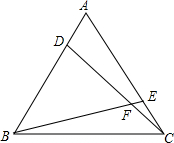 如图,D、E分别是等边△ABC的两条边AB、AC上的点,且AD=CE,求∠DFB的度数.
如图,D、E分别是等边△ABC的两条边AB、AC上的点,且AD=CE,求∠DFB的度数.