题目内容
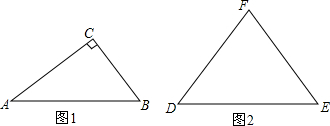
7.定义:如果三角形某一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”(1)如图1,在Rt△ABC中,∠C=90°,tanA=$\frac{\sqrt{3}}{2}$,求证:△ABC是“好玩三角形”;
(2)如图2,若等腰△DEF是“好玩三角形”,DF=EF,求腰和底的比值.
分析 (1)取AC的中点D,连接BD,设BC=$\sqrt{3}$x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BD,从而得出结论;
(2)如图2,取DE的中点G,连接FG,则由“好玩三角形”的定义得到FG=DE,则由勾股定理可以求得FD的长度,然后求腰和底的比值即可.
解答 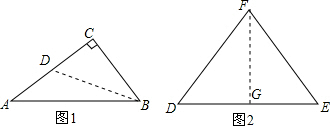 (1)证明:如图1,取AC的中点D,连接BD,
(1)证明:如图1,取AC的中点D,连接BD,
∵∠C=90°,tanA=$\frac{\sqrt{3}}{2}$,
∴$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,
∴设BC=$\sqrt{3}$x,则AC=2x,
∵D是AC的中点,
∴CD=$\frac{1}{2}$AC=x
∴BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{3{x}^{2}+{x}^{2}}$=2x,
∴AC=BD,
∴△ABC是“好玩三角形”;
(2)①如图2,取DE的中点G,连接FG,则FG=DE.
∵DF=EF,
∴DG=$\frac{1}{2}$DE=$\frac{1}{2}$FG,FG⊥DE,
在直角△FDG中,由勾股定理得到:FD=$\sqrt{D{G}^{2}+F{G}^{2}}$=$\sqrt{5}$DG,
∴$\frac{FD}{DE}$=$\frac{\sqrt{5}DG}{2DG}$=$\frac{\sqrt{5}}{2}$,即腰和底的比值是$\frac{\sqrt{5}}{2}$.
②取EF的中点M,连接DM,由题意知DM=EF=DF,作DH垂直EF于H,则FH=MH,设FH=MH=1,则ME=2,DF=4,
在Rt△DFH中,根据勾股定理得:DH2=15,
在Rt△DEH中,根据勾股定理得:DE=2$\sqrt{6}$,从而可得腰与底的比为:$\sqrt{6}$:3.
综上所述,腰和底的比值是$\frac{\sqrt{5}}{2}$或$\frac{\sqrt{6}}{3}$.
点评 本题考查了勾股定理的运用,等腰直角三角形的性质的运用,等腰三角形的性质的运用,锐角三角形函数值的运用,解答时灵活运用三角函数值建立方程求解是解答的关键.

| A. | 5 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | ±$\sqrt{5}$ |
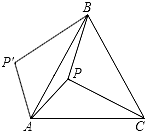 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$. 请建立适当的平面直角坐标系,写出边长为4的等边△ABC的各顶点坐标.
请建立适当的平面直角坐标系,写出边长为4的等边△ABC的各顶点坐标.