题目内容
2. 请建立适当的平面直角坐标系,写出边长为4的等边△ABC的各顶点坐标.
请建立适当的平面直角坐标系,写出边长为4的等边△ABC的各顶点坐标.
分析 以BC所在的直线为x轴,以BC边上的高所在的直线为y轴,建立平面直角坐标系,则BO=CO,再根据勾股定理求出AO的长度,点A、B、C的坐标即可写出.
解答 解:如图,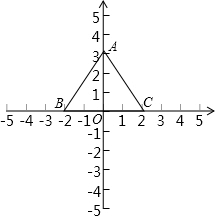
以BC所在的直线为x轴,以BC边上的高所在的直线为y轴,建立平面直角坐标系,
∵正三角形ABC的边长为4,
∴BO=CO=2,
∴点B、C的坐标分别为B(-2,0),C(2,0),
∵AO=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴点A的坐标为(0,2$\sqrt{3}$).
点评 本题主要考查坐标与图形的性质,等边三角形的性质,勾股定理的运用,建立适当的平面直角坐标系是解题的关键.

练习册系列答案
相关题目
12.已知点C是线段AB的黄金分割点,且CB>AC,则下列等式中成立的是( )
| A. | AB2=AC•CB | B. | CB2=AC•AB | C. | AC2=CB•AB | D. | AC2=2BC•AB |
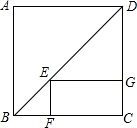 如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.
如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.