题目内容

12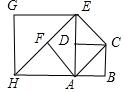．如图，在边长为1的正方形ABCD中，连结对角线AC，以AC为边作第二个正方形，连结对角线AE，以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是（　　）
A．22016B．22016$\sqrt{2}$C．21008D．21008$\sqrt{2}$

分析 首先求出AC、AE、HE的长度，然后猜测命题中隐含的数学规律，即可解决问题．

解答 解：∵四边形ABCD为正方形，
∴AB=BC=1，∠B=90°，
∴AC2=12+12，AC=$\sqrt{2}$；
同理可求：AE=（$\sqrt{2}$）2，HE=（$\sqrt{2}$）3…，
∴第n个正方形的边长an=$（\sqrt{2}）^{n-1}$．
第2017个正方形的边长是21008，
故选C

点评 该题主要考查了正方形的性质、勾股定理及其应用问题；应牢固掌握正方形有关定理并能灵活运用．

练习册系列答案
相关题目
2．盒子里装有若干个红球、绿球和5个黄球，它们除颜色外完全相同，从盒子中任意摸出一个球，摸到黄球的概率是$\frac{1}{10}$．
（1）三种颜色的球共有多少个？
（2）若摸到红球的概率与摸到绿球的概率之比是4：5，红球和绿球的个数分别有多少个？
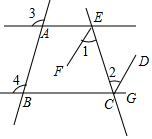3．已知：如图，直线AE，BC被直线AB，EC所截，已知∠3=∠4，EF平分∠AEC，CD平分∠ECG，将下列证明EF∥CD的过程及理由填写完整．
证明：∵∠3=∠4
∴AE∥BC（同位角相等，两直线平行）
∴∠AEC=∠ECG，（两直线平行，内错角相等）
∵EF平分∠AEC，CD平分∠ECG
∴∠1=$\frac{1}{2}$∠AEC，∠2=$\frac{1}{2}$∠AEC
∴∠1=∠2
∴EF∥CD（内错角相等，两直线平行）．
20．一个圆柱的高为8cm，则圆柱体的体积Vcm3与底面直径Rcm的关系式为V=2πR2，当R为5cm时，V=50πcm3．
7．如图，已知：AB∥CD，不添加辅助线，试再添加一个条件，使∠1=∠2成立．
要求：（1）写出两个答案；（2）选择其中一个加以证明．
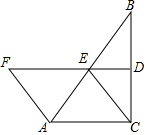17．如图，∠ACB=90°，D，E分别为BC，AB的中点，DE的延长线交AF于F，∠F=∠FEA．
（1）求证：四边形ACEF为平行四边形；
（2）当∠B=30°时，四边形ACEF是菱形．
4．若2a=3，2b=5，则23a+2b等于675．
1．（1）解方程：（x+1）2=64；
（2）计算：（-2）3×$\sqrt{（-4）^{2}}$+$\root{3}{（-4）^{3}}$×（$\frac{1}{2}$）2-$\sqrt{9}$．
2．列方程组解应用题：
在“某地大地震”灾民安置工作中，某企业捐助了一批板材24 000m2，某灾民安置点用该企业捐助的这批板材全部搭建成A，B两种型号的板房，供2 300名灾民临时居住．已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示：
板房型号所需板材安置人数
A型板房54m25
B型板房78m28
问：（1）该灾民安置点需搭建A型板房和B型板房各多少间？
（2）因对灾民人数估计不足，实际安置中A型板房超员15%，B型板房超员20%，则该安置点灾民实际有多少人？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网