题目内容
7. 如图,已知:AB∥CD,不添加辅助线,试再添加一个条件,使∠1=∠2成立.
如图,已知:AB∥CD,不添加辅助线,试再添加一个条件,使∠1=∠2成立.要求:(1)写出两个答案;(2)选择其中一个加以证明.
分析 根据平行线的性质可得:∠BAH=∠AHC,要使∠1=∠2,只要使∠EAH=∠FHA即可,只要添加AE∥FH即可.
解答  解:(1)AE∥FH;∠EAH=∠FHA;∠E=∠F(写出两个即可);
解:(1)AE∥FH;∠EAH=∠FHA;∠E=∠F(写出两个即可);
(2)选择:AE∥FH.
证明:因为AB∥CD,
所以∠BAH=∠CHA,
又因为AE∥FH,
所以∠EAH=∠FHA,
所以∠BAH-∠EAH=∠CHA-∠FHA,
即∠1=∠2.
点评 本题考查了平行线的性质,此类题要首先根据已知条件进行推理,再结合结论和所学过的性质进行推导.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.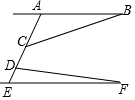 如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
 如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )| A. | 38° | B. | 40° | C. | 55° | D. | 60° |
12.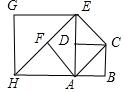 如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )
如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )
 如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )
如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )| A. | 22016 | B. | 22016$\sqrt{2}$ | C. | 21008 | D. | 21008$\sqrt{2}$ |

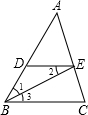 如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程.
如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程.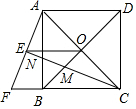 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=2$\sqrt{2}$.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=2$\sqrt{2}$.