题目内容
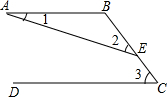如图，AB∥CD，E是BD上的一点．下列结论中，正确的是（ ）| A、∠1=∠2-∠3 |
| B、∠2=∠1-∠3 |
| C、∠3=∠1+∠2 |
| D、∠1+∠2+∠3=180° |
考点：平行线的性质
专题：
分析：根据两直线平行，同旁内角互补即可得到∠3+∠B=180°，然后在△ABE中利用三角形的内角和定理即可判断．
解答：解：∵AB∥CD，
∴∠3+∠B=180°，
又∵∠1+∠2+∠B=180°，
∴∠3=∠1+∠2．
故选C．
∴∠3+∠B=180°，
又∵∠1+∠2+∠B=180°，
∴∠3=∠1+∠2．
故选C．
点评：本题考查了平行线的性质定理以及三角形的内角和定理，正确理解定理是关键．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
用求差法比较大小，就是根据两数之差是正数、负数或0，判断两数大小关系的方法．若a＞b，m＞n，试比较P=n-5a与Q=m-5b的大小为（ ）
| A、P＜Q | B、P＞Q |
| C、P=Q | D、P与Q的大小不确定 |
下列说法中错误的是（ ）
| A、平行四边形两条对角线互相平分 |
| B、矩形两条对角线垂直 |
| C、正方形两条对角线垂直且相等 |
| D、菱形两条对角线互相垂直 |
甲、乙、丙、丁四名同学在讨论数学问题时作了如下发言：
甲：因为三角形中最多有一个钝角，因此三角形的外角之中最多只有一个锐角；
乙：在求n个角都相等的n边形的一个内角的度数时，可用结论：180°-
×360°；
丙：多边形的内角和总比外角和大；
丁：n边形的边数每增加一条，对角线就增加n条．
四位同学的说法正确的是（ ）
甲：因为三角形中最多有一个钝角，因此三角形的外角之中最多只有一个锐角；
乙：在求n个角都相等的n边形的一个内角的度数时，可用结论：180°-
| 1 |
| n |
丙：多边形的内角和总比外角和大；
丁：n边形的边数每增加一条，对角线就增加n条．
四位同学的说法正确的是（ ）
| A、甲、丙 | B、乙、丁 |
| C、甲、乙 | D、乙、丙 |
若用配方法解方程x2-4x=1，则方程两边都加上（ ）
| A、4 | B、3 | C、2 | D、1 |
如图的曲线表示周末班主任带学生步行去动物园游玩的情况，图象表示学生离校的距离y千米与从出发开始第x小时的关系．根据这个图象，回答下列问题：