题目内容
下列说法中错误的是（ ）
| A、平行四边形两条对角线互相平分 |
| B、矩形两条对角线垂直 |
| C、正方形两条对角线垂直且相等 |
| D、菱形两条对角线互相垂直 |
考点：正方形的性质,平行四边形的性质,菱形的性质,矩形的性质
专题：
分析：分别根据平行四边形的性质、矩形及正方形的性质、菱形的性质对各选项进行逐一分析即可．
解答：解：A、平行四边形两条对角线互相平分符合平行四边形的性质，原来的说法正确，不符合题意；
B、矩形两条对角线相等且互相平分，但不垂直，原来的说法错误，符合题意；
C、正方形两条对角线垂直且相等，符合正方形的性质，原来的说法正确，不符合题意；
D、菱形两条对角线互相垂直，符合菱形的性质，原来的说法正确，不符合题意．
故选B．
B、矩形两条对角线相等且互相平分，但不垂直，原来的说法错误，符合题意；
C、正方形两条对角线垂直且相等，符合正方形的性质，原来的说法正确，不符合题意；
D、菱形两条对角线互相垂直，符合菱形的性质，原来的说法正确，不符合题意．
故选B．
点评：本题考查的是正方形的性质，熟知平行四边形、矩形、正方形、菱形的对角线的特点是解答此题的关键．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
|
A、
| ||||
B、±
| ||||
C、
| ||||
D、±
|
如图，正方形内部分布着一个大正方形和三个边长相等的小正方形，设左下角较大的正方形的面积为S1，三个小正方形中的其中一个正方形的面积为S2，那么S1，S2的比值是（ ）| A、3：1 | ||
| B、4：1 | ||
| C、25：8 | ||
D、5：2
|
红星中学七年级一班学生在本学期参加4种课外兴趣小组情况的统计图如图，则参加人数最多的课外兴趣小组是（ ）| A、硬笔书法 | B、中国象棋 |
| C、艺术体操 | D、美术写生 |
以下四个命题：
①在同一平面内，过一点有且只有一条直线与已知直线垂直；
②若a＞b，则-2a＞-2b；
③如果三条直线a、b、c满足：a∥b，b∥c，那么直线a与直线c必定平行；
④对顶角相等．
其中真命题有（ ）个．
①在同一平面内，过一点有且只有一条直线与已知直线垂直；
②若a＞b，则-2a＞-2b；
③如果三条直线a、b、c满足：a∥b，b∥c，那么直线a与直线c必定平行；
④对顶角相等．
其中真命题有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
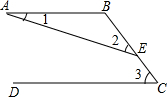如图，AB∥CD，E是BD上的一点．下列结论中，正确的是（ ）| A、∠1=∠2-∠3 |
| B、∠2=∠1-∠3 |
| C、∠3=∠1+∠2 |
| D、∠1+∠2+∠3=180° |