题目内容
(1)如图(1),点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:△BCP≌△DCE;
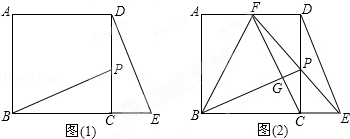
(2)如图(2),直线EP交AD于F,连接BF,FC.FC与BP交与点G.
①若点P是CD中点时,判断CF与BP的关系,并说明理由.
②若CD=4,CP=1,求△BPF的面积和△DPE的面积.
③若CD=n•PC(n是大于1的实数)时,记△BPF的面积为S1,△DPE的面积为S2.则
= (不需要证明)

(2)如图(2),直线EP交AD于F,连接BF,FC.FC与BP交与点G.
①若点P是CD中点时,判断CF与BP的关系,并说明理由.
②若CD=4,CP=1,求△BPF的面积和△DPE的面积.
③若CD=n•PC(n是大于1的实数)时,记△BPF的面积为S1,△DPE的面积为S2.则
| S1 |
| S2 |
考点:四边形综合题
专题:
分析:(1)利用SAS,证明△BCP≌△DCE;
(2)在(1)的基础上,再证明△BCP≌△CDF,进而得到CF=BP,∠FCD+∠BPC=90°,从而证明BP⊥CF;
②△BPF的面积=△BFE的面积-△BPE的面积,△DPE的面积=△DCE的面积-△PCE的面积,依此计算即可求解;
③设CP=CE=1,则BC=CD=n,DP=CD-CP=n-1,分别求出S1与S2的值,得S1=
(n2-1),S2=
(n-1),所以
=(n+1).
(2)在(1)的基础上,再证明△BCP≌△CDF,进而得到CF=BP,∠FCD+∠BPC=90°,从而证明BP⊥CF;
②△BPF的面积=△BFE的面积-△BPE的面积,△DPE的面积=△DCE的面积-△PCE的面积,依此计算即可求解;
③设CP=CE=1,则BC=CD=n,DP=CD-CP=n-1,分别求出S1与S2的值,得S1=
| 1 |
| 2 |
| 1 |
| 2 |
| S1 |
| S2 |
解答:证明:(1)在△BCP与△DCE中,
,
∴△BCP≌△DCE(SAS).
(2)①答:CF=BP,CF⊥BP.
∵CP=CE,∠PCE=90°,
∴∠CPE=45°,
∴∠FPD=∠CPE=45°,
∴∠PFD=45°,
∴FD=DP.
∵CD=2PC,
∴DP=CP,
∴FD=CP.
在△BCP与△CDF中,
,
∴△BCP≌△CDF(SAS).
∴BP=CF,∠FCD=∠CBP,
∵∠CBP+∠BPC=90°,
∴∠FCD+∠BPC=90°,
∴∠PGC=90°,即BP⊥CF.
故CF与BP的关系:CF=BP,CF⊥BP.
②△BPF的面积=△BFE的面积-△BPE的面积
=
×(4+1)×4-
×1×1
=10-2.5
=7.5,
△DPE的面积=△DCE的面积-△PCE的面积
=
×4×1-
×(4+1)×1
=2-0.5
=1.5
故△BPF的面积为7.5,△DPE的面积为1.5.
③设CP=CE=1,则BC=CD=n,DP=CD-CP=n-1.
易知△FDP为等腰直角三角形,
∴FD=DP=n-1.
S1=S梯形BCDF-S△BCP-S△FDP
=
(BC+FD)•CD-
BC•CP-
FD•DP
=
(n+n-1)•n-
n×1-
(n-1)2
=
(n2-1);
S2=
DP•CE=
(n-1)×1=
(n-1).
∵n2-1=(n+1)(n-1),
∴
=n+1.
故答案为:n+1.
|
∴△BCP≌△DCE(SAS).
(2)①答:CF=BP,CF⊥BP.
∵CP=CE,∠PCE=90°,
∴∠CPE=45°,
∴∠FPD=∠CPE=45°,
∴∠PFD=45°,
∴FD=DP.
∵CD=2PC,
∴DP=CP,
∴FD=CP.
在△BCP与△CDF中,
|
∴△BCP≌△CDF(SAS).
∴BP=CF,∠FCD=∠CBP,
∵∠CBP+∠BPC=90°,
∴∠FCD+∠BPC=90°,
∴∠PGC=90°,即BP⊥CF.
故CF与BP的关系:CF=BP,CF⊥BP.
②△BPF的面积=△BFE的面积-△BPE的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=10-2.5
=7.5,
△DPE的面积=△DCE的面积-△PCE的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=2-0.5
=1.5
故△BPF的面积为7.5,△DPE的面积为1.5.
③设CP=CE=1,则BC=CD=n,DP=CD-CP=n-1.
易知△FDP为等腰直角三角形,
∴FD=DP=n-1.
S1=S梯形BCDF-S△BCP-S△FDP
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵n2-1=(n+1)(n-1),
∴
| S1 |
| S2 |
故答案为:n+1.
点评:本题是几何综合题,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形、图形的面积等知识点,试题的综合性较强,难度中等.

练习册系列答案
相关题目
|
A、
| ||||
B、±
| ||||
C、
| ||||
D、±
|
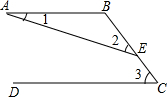 如图,AB∥CD,E是BD上的一点.下列结论中,正确的是( )
如图,AB∥CD,E是BD上的一点.下列结论中,正确的是( )| A、∠1=∠2-∠3 |
| B、∠2=∠1-∠3 |
| C、∠3=∠1+∠2 |
| D、∠1+∠2+∠3=180° |
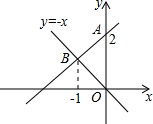 如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,
如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,