题目内容
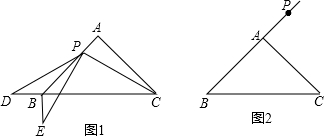
6. 如图,已知∠1=∠2,∠3+∠4=180°,证明AB∥EF.
如图,已知∠1=∠2,∠3+∠4=180°,证明AB∥EF.
分析 根据∠1=∠2利用“同位角相等,两直线平行”可得出AB∥CD,再根据∠3+∠4=180°利用“同旁内角互补,两直线平行”可得出CD∥EF,从而即可证出结论.
解答 证明:∵∠1=∠2,
∴AB∥CD.
∵∠3+∠4=180°,
∴CD∥EF.
∴AB∥EF.
点评 本题考查了平行线的判定,解题的关键是分别找出AB∥CD、CD∥EF.本题属于基础题,难度不大,解决该题型题目时,根据相等或互补的角找出平行的直线是关键.

练习册系列答案
相关题目
14.若(x+3)(x+n)=x2+mx-15,则m的值为( )
| A. | -5 | B. | -2 | C. | 5 | D. | 2 |
11.对于任意实数x,下列各式中一定成立的是( )
| A. | $\sqrt{{x}^{2}-1}$=$\sqrt{x-1}$•$\sqrt{x+1}$ | B. | $\sqrt{{(x+1)}^{2}}$=x+1 | C. | $\sqrt{(-4)•(-x)}$=$\sqrt{-4}$•$\sqrt{-x}$ | D. | $\sqrt{3{6x}^{4}}$=6x2 |
18. 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>5}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<5}\\{x≥-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>5}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<5}\\{x>-1}\end{array}\right.$ |
15.不等式4+2x>0的解集是( )
| A. | 2x>4 | B. | x>2 | C. | x>-2 | D. | x<-2 |
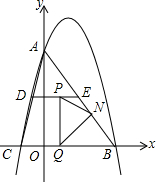 如图,已知抛物线y=-$\frac{4}{3}$x2+bx+c经过A(0,4),B(3,0)两点,与x轴负半轴交于点C,连接AC、AB.
如图,已知抛物线y=-$\frac{4}{3}$x2+bx+c经过A(0,4),B(3,0)两点,与x轴负半轴交于点C,连接AC、AB.