题目内容
1．已知n是关于x的一元二次方程x2+m2x-2m=0（m为实数）的一个实数根，则n的最大值是1．分析 由n是方程的根可得nm2-2m+n2=0且△=（-2）2-4n•n2≥0，继而可得n的取值范围，即可知n的最大值．
解答 解：∵n是方程x2+m2x-2m=0（m为实数）的一个实数根，
∴nm2-2m+n2=0，且△=（-2）2-4n•n2≥0，
即4-4n3≥0，
∴n3≤1，
则n≤1，
∴n的最大值为1，
故答案为：1．
点评 本题主要考查一元二次方程的解与根的判别式，根据题意得出关于n的不等式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11．对于任意实数x，下列各式中一定成立的是（ ）
| A． | $\sqrt{{x}^{2}-1}$=$\sqrt{x-1}$•$\sqrt{x+1}$ | B． | $\sqrt{{（x+1）}^{2}}$=x+1 | C． | $\sqrt{（-4）•（-x）}$=$\sqrt{-4}$•$\sqrt{-x}$ | D． | $\sqrt{3{6x}^{4}}$=6x2 |
9．下列关于$\sqrt{8}$的说法中，错误的是（ ）
| A． | $\sqrt{8}$是8的算术平方根 | B． | 2＜$\sqrt{8}$＜3 | ||
| C． | $\sqrt{8}$=$±2\sqrt{2}$ | D． | $\sqrt{8}$是无理数 |
6．
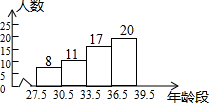菲尔兹奖（Fields Medal）是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家，下面是对截至2015年56名获奖者的年龄进行统计得到的统计图．则下列说法中正确的是（ ）
菲尔兹奖（Fields Medal）是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家，下面是对截至2015年56名获奖者的年龄进行统计得到的统计图．则下列说法中正确的是（ ）| A． | 平均年龄是37.5岁 | B． | 中位数年龄位于33.5-36.5岁 | ||
| C． | 众数年龄位于36.5-39.5岁 | D． | 以上选项都不正确 |
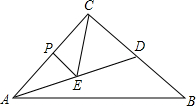如图，在Rt△ABC中，∠C=90°，AC=4，BC=5，D是BC边上一点，CD=3，P是AC边上一动点（不与A、C重合），过点P作PE∥BC交AD于点E，将△ABD沿直线AD翻折，得到△AB′D，连接B′C，当∠ACE=∠BCB′时，则AE=$\frac{64}{25}$．
类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
6．
如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=32°，则∠2的度数为（ ）
如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=32°，则∠2的度数为（ ）| A． | 25° | B． | 28° | C． | 30° | D． | 32° |