题目内容
2.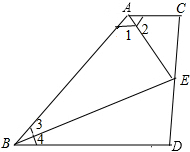 如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.
如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.
分析 过E点作EF∥BC,根据梯形中位线定理,可得EF∥AD∥BC,AF=BF,根据平行线的性质得到∠2=∠5,再根据等式的性质和等角对等边得到AF=EF,根据等量关系得到BF=EF,根据等边对等角得到∠3=∠6,再根据平行线的性质得到∠4=∠6,再根据等量关系即可求解.
解答  证明:过E点作EF∥BC,
证明:过E点作EF∥BC,
∵E为CD的中点,AD∥BC,
∴EF∥AD∥BC,AF=BF,
∴∠2=∠5,∠4=∠6,
∵∠1=∠2,
∴∠1=∠5,
∴AF=EF,
∴BF=EF,
∴∠3=∠6,
∴∠3=∠4.
点评 此题考查平行线的性质,梯形中位线定理,关键是得到梯形ABCD的中位线等于AB的一半.

练习册系列答案
相关题目
14.2013年4月20日,四川省雅安市芦山县发生了7.0级大地震,给当地居民造成了巨大的损失,“一方有难,八方支援”,某市中学全体师生积极捐款,其中九年级3个班学生的捐款金额如下表:
吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面两条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:九(2)班的捐款金额比九(3)班的捐款金额多300元.
请根据以上信息求出九(2)班与九(3)班的捐款金额各是多少元.
| 班级 | 九(1)班 | 九(2)班 | 九(3)班 |
| 金额/元 | 2000 |
信息一:这三个班的捐款总金额是7700元;
信息二:九(2)班的捐款金额比九(3)班的捐款金额多300元.
请根据以上信息求出九(2)班与九(3)班的捐款金额各是多少元.
 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V. 如图,半径为5的⊙O中,OD⊥AB,连接AD,AD=2$\sqrt{5}$,则AB=8.
如图,半径为5的⊙O中,OD⊥AB,连接AD,AD=2$\sqrt{5}$,则AB=8.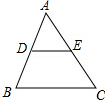 如图,在△ABC中,已知DE∥BC,AD=5,DB=3,BC=10,求:
如图,在△ABC中,已知DE∥BC,AD=5,DB=3,BC=10,求: