题目内容
2.已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数y=x+3的图象与x轴,y轴的交点,并也经过(1,1)点.(1)分别求出一次函数y=x+3与x轴、y轴的交点;
(2)求这个二次函数解析式;
(3)求x为何值时,二次函数有最大(最小)值,这个值是什么?
分析 (1)分别令一次函数x=0,y=0求出其与x轴、y轴的交点;
(2)把三点代入二次函数的解析式,用待定系数法求出二次函数的解析式.
(2)把二次函数化成顶点式,利用性质求得最值即可.
解答 解:(1)令x=0,得y=3,令y=0,得x=-3,
一次函数y=x+3与x轴、y轴的交点坐标为(-3,0),(0,3),
(2)把(0,3),(-3,0),(1,1)分别代入y=ax2+bx+c,得
$\left\{\begin{array}{l}{c=3}\\{9a-3b+c=0}\\{a+b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
这个二次函数解析式y=-x2-2x+3;
(3)y=-x2-2x+3=-(x+1)2+4,
a=-1<0,抛物线开口向下,当x=-1时,二次函数有最大值,这个值是4.
点评 此题主要考查一次函数和二次函数的性质,一次函数与x轴、y轴的交点坐标,用待定系数法求出二次函数的解析式的方法.

练习册系列答案
相关题目
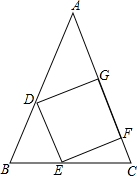 已知,如图,正方形DEFG的一边FG在等腰△ABC的腰AC上,AB=AC=5,顶点D、E分别为边AB、BC上,△ABC的面积为10,求正方形DEFG的面积.
已知,如图,正方形DEFG的一边FG在等腰△ABC的腰AC上,AB=AC=5,顶点D、E分别为边AB、BC上,△ABC的面积为10,求正方形DEFG的面积.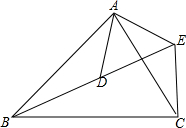 如图,AB:AD=BC:DE=AC:AE.
如图,AB:AD=BC:DE=AC:AE.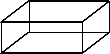 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V.