题目内容
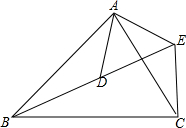
20. 如图,C为△ABE的边BE上,且AB=AC,AB的垂直平分线交AC于D,且AD=BC,CE=CD.
如图,C为△ABE的边BE上,且AB=AC,AB的垂直平分线交AC于D,且AD=BC,CE=CD.(1)求∠BAC的度数;
(2)求∠CAE的度数.
分析 (1)根据线段垂直平分线的性质得到DA=DB,根据题意得到∠ABC=∠ACB,设∠BAC=x,根据三角形内角和定理列出方程,解方程得到答案;
(2)连接DE,根据三角形的外角的性质求出∠CDE=∠CED=$\frac{1}{2}$∠ACB=36°,证明DA=DE,得到答案.
解答  解:(1)∵AB的垂直平分线交AC于D,
解:(1)∵AB的垂直平分线交AC于D,
∴DA=DB,
∴∠DAB=∠DBA,
∵AD=BC,DA=DB,
∴BC=DB,
∴∠BDC=∠BCD,
∵AB=AC,
∴∠ABC=∠ACB,
设∠BAC=x,则∠ABC=∠ACB=2x,
则x+2x+2x=180°,
解得,x=36°,
即∠BAC为36°,
(2)连接DE,
∵CE=CD,
∴∠CDE=∠CED=$\frac{1}{2}$∠ACB=36°,
∴DB=DE,又DA=DB,
∴DA=DE,
∴∠CAE=$\frac{1}{2}$∠CDE=18°.
点评 本题考查的是线段垂直平分线的性质、等腰三角形的性质和三角形的外角的性质,正确作出辅助线、掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15.如果4a2+1与一个单项式的和恰好是一个整式的平方,那么这样的单项式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
 如图,AB:AD=BC:DE=AC:AE.
如图,AB:AD=BC:DE=AC:AE. 如图,轮船B在灯塔A北偏东40°方向,轮船C在轮船B南偏东40°方向,如果∠ABC=∠C.通过计算说明轮船C在灯塔A的什么方向?
如图,轮船B在灯塔A北偏东40°方向,轮船C在轮船B南偏东40°方向,如果∠ABC=∠C.通过计算说明轮船C在灯塔A的什么方向? 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V.