题目内容
19. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.(1)求证:DF为⊙O的切线;
(2)求证:CD2=AB•EF.
分析 (1)根据等腰三角形的性质,于是可判断OD∥AC,由于DF⊥AC,所以OD⊥DF,然后根据切线的判定定理即可得到结论;
(2)连接DE,根据等腰三角形的性质得到∠B=∠C,等量代换得到∠DEF=∠C,求得DE=DC,推出CF=EF,通过△CDF∽△CAD,得到$\frac{CD}{CF}=\frac{CA}{CD}$,即可得到结论.
解答 证明:(1)连接OD,AD,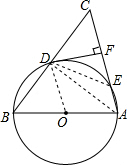 ∵AB=AC,AB为⊙O的直径,
∵AB=AC,AB为⊙O的直径,
∴AD⊥BC,BD=CD,
∵AO=BO,
∴OD∥AC,
∵DF⊥AC于F,
∴OD⊥DF,
∴DF为⊙O的切线;
(2)连接DE,则∠B=∠DEF,
∵AB=AC,
∴∠B=∠C,
∴∠DEF=∠C,
∴DE=DC,
∴CF=EF,
在Rt△ADC中,DF⊥AC,
∴∠CFD=∠ADC=90°,
∵∠C=∠C,
∴△CDF∽△CAD,
∴$\frac{CD}{CF}=\frac{CA}{CD}$,
∴CD2=CF•CA
即CD2=AB•EF.
点评 本题考查了相似三角形的判定和性质,切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理.

练习册系列答案
相关题目
7. 如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
 如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )| A. | 68° | B. | 102° | C. | 110° | D. | 112° |
4.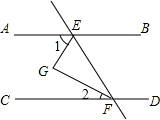 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )| A. | 40° | B. | 35° | C. | 25° | D. | 20° |
11.安徽人不仅爱网购,网上销售做得也越来越好.省统计局2015年8月28日发布的数据显示,2015年1~7月份,安徽省限额以上批发零售业实现网上商品零售额60.8亿元,总量位居中部第二,同比增长66.1%.其中60.8亿用科学记数法表示为( )
| A. | 60.8×108 | B. | 6.08×109 | C. | 6.8×109 | D. | 608.8×107 |
 如图,一次函数y=kx+b分别与x轴、y轴交于A,B两点,与反比例函数y=-$\frac{4}{x}$交于点C,B为AC的中点,则△AOC的面积为2.
如图,一次函数y=kx+b分别与x轴、y轴交于A,B两点,与反比例函数y=-$\frac{4}{x}$交于点C,B为AC的中点,则△AOC的面积为2.