题目内容
16. 已知:四边形ABCD是平行四边形,BE平分∠ABC交AD于E,∠AEB=30°,AE=4cm.
已知:四边形ABCD是平行四边形,BE平分∠ABC交AD于E,∠AEB=30°,AE=4cm.(1)求∠C的度数和CD的长;
(2)若BC=6,求S?ABCD.
分析 (1)由四边形ABCD是平行四边形,BE平分∠ABC,易证得△ABE是等腰三角形,继而求得答案;
(2)首先过点A作AF⊥BC于点F,可得△ABF是含30°角的直角三角形,继而求得答案.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,∠C=∠A,
∴∠CBE=∠AEB=30°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=30°,
∴∠ABE=∠AEB,
∴AB=AE=4cm,
∴CD=AB=4cm;
∴∠A=180°-∠ABE-∠AEB=120°,
∴∠C=120°;
(2)过点A作AF⊥BC于点F,
∵AD∥BC,∠BAD=120°,
∴∠ABC=180°-∠BAD=60°,
∴∠BAF=90°-∠ABC=30°,
∴BF=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2(cm),
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=2$\sqrt{3}$(cm),
∴S?ABCD=BC•AF=6×2$\sqrt{3}$=12$\sqrt{3}$.
点评 此题考查了平行四边形的性质、勾股定理、等腰三角形的判定与性质以及含30°角的直角三角形的性质.注意证得△ABE是等腰三角形,准确作出辅助线是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若计算(x-5)(x+a)的结果是x2-bx-10,则a的值是( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
4. 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④AB=HF,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.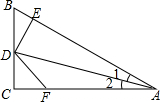 如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
 如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )| A. | ∠1=∠2 | B. | DE=DF | C. | BD=FD | D. | AB=AC |
9.在如图所示的2014年2月份日历中,用一个长方形的方框圈出任意2×2个数,例如:圈出2、3、9、10四个数.
(1)在日历表像这样圈出的四个数中,最小的数假设为x,那么最大的数是x+8(用含x的式子表示);
(2)在2014年3月份日历表,圈出的四个数和为96,则这四个数中最大的为28.
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
(2)在2014年3月份日历表,圈出的四个数和为96,则这四个数中最大的为28.
 如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由.
如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由. 已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.