题目内容
11.已知D、E是△ABC的AB,AC边上的中点,DE=2cm,AB+AC=12cm,则BC=4cm,四边形DBCE的周长是12cm.分析 由三角形中位线定理可求得BC=2DE,结合中点的定义可知BD+EC=$\frac{1}{2}$(AB+AC),可求得四边形DBCE的周长.
解答 解:
∵D、E是△ABC的AB、AC边上的中点,
∴DE是△ABC的BC边上的中位线,
∴BC=2DE=4cm,
∵D、E分别是AB、AC的中点,
∴AB=2BD,AC=2CE,
∴2BD+2CE=12cm,
∴BD+EC=6cm,
∴DE+BC+BD+EC=2+4+6=12(cm),
故答案为:4;12.
点评 本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
3.已知x=3y=6z=-2014,则x+y+z+2014是( )
| A. | 正数 | B. | 零 | C. | 负数 | D. | 无法确定 |
 已知:四边形ABCD是平行四边形,BE平分∠ABC交AD于E,∠AEB=30°,AE=4cm.
已知:四边形ABCD是平行四边形,BE平分∠ABC交AD于E,∠AEB=30°,AE=4cm.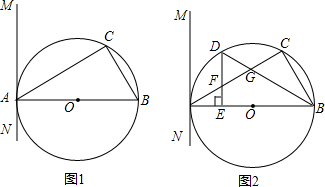
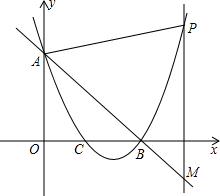 如图,已知抛物线y=x2+bx+c与直线y=-x+3交于A、B两点,点A 在y轴上,点B在x轴上,抛物线与x轴的另一交点为C,点P在点B右边的抛物线上,PM⊥x轴交直线AB于M.
如图,已知抛物线y=x2+bx+c与直线y=-x+3交于A、B两点,点A 在y轴上,点B在x轴上,抛物线与x轴的另一交点为C,点P在点B右边的抛物线上,PM⊥x轴交直线AB于M.