题目内容
14．函数y=kx-1（常数k＞0）的图象不经过的象限是（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 一次函数y=kx-1（常数k＞0）的图象一定经过第一、三，四象限，不经过第二象限．
解答 解：∵一次函数y=kx-1（常数k＞0），b=-1＜0，
∴一次函数y=kx-1（常数k＞0）的图象一定经过第一、三，四象限，不经过第二象限．
故选：B．
点评 本题主要考查了函数图象上的点与图象的关系，图象上的点满足解析式，满足解析式的点在函数图象上．并且本题还考查了一次函数的性质，都是需要熟记的内容．
练习册系列答案
相关题目
4．已知点P在第四象限，且到x轴的距离是2，到y轴的距离是3，则点P的坐标为（ ）
| A． | （2，-3） | B． | （-3，2） | C． | （3，-2） | D． | （-2，3） |
5．若-4≤x≤3，化简$\sqrt{{x}^{2}+8x+16}$-$\sqrt{{x}^{2}-6x+9}$的结果为（ ）
| A． | 2x+1 | B． | -2x-1 | C． | 1 | D． | 7 |
2．
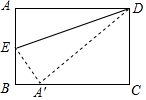一张矩形纸片ABCD，AD=5cm，AB=3cm，将纸片沿ED折叠，A点刚好落在BC边上的A'处，如图，这时AE的长应该是（ ）
一张矩形纸片ABCD，AD=5cm，AB=3cm，将纸片沿ED折叠，A点刚好落在BC边上的A'处，如图，这时AE的长应该是（ ）| A． | $\frac{5}{3}$cm | B． | $\frac{4}{3}$cm | C． | $\frac{3}{2}$cm | D． | $\frac{7}{5}$cm |
9．在平面直角坐标系中，点A在第一象限，点B在x轴正半轴上，∠AOB=60°，OA=8．点A的坐标是（ ）
| A． | （4，8） | B． | （4，4 $\sqrt{3}$） | C． | （4$\sqrt{3}$，4） | D． | （8，4） |
19．如果将抛物线y=x2+2向右平移1个单位，那么所得新抛物线的表达式是（ ）
| A． | y=x2+3 | B． | y=（x-1）2+2 | C． | y=（x+1）2+2 | D． | y=x2+1 |
6．
如图，两条宽度都是1的纸条，交叉重叠放在一起，且夹角为α，则重叠部分的面积为（ ）
如图，两条宽度都是1的纸条，交叉重叠放在一起，且夹角为α，则重叠部分的面积为（ ）| A． | $\frac{1}{sinα}$ | B． | $\frac{1}{cosα}$ | C． | tanα | D． | 1 |
3．
如图，菱形ABCD的对角线AC，BD相交于点O，AC=8cm，BD=6cm，AC上一动点P从点C出发，沿CA方向以1cm/s的速度向A运动，设点P运动时间为ts．当t等于（ ）时，△PCD是直角三角形．
如图，菱形ABCD的对角线AC，BD相交于点O，AC=8cm，BD=6cm，AC上一动点P从点C出发，沿CA方向以1cm/s的速度向A运动，设点P运动时间为ts．当t等于（ ）时，△PCD是直角三角形．| A． | $\frac{9}{4}$s | B． | 4s | C． | $\frac{9}{4}$s或$\frac{25}{4}$s | D． | 4s或$\frac{25}{4}$s |
4．若xm=16，xn=4，则x2m-3n的值为（ ）
| A． | 192 | B． | 8 | C． | -32 | D． | 4 |