题目内容
1.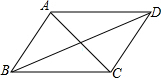 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )| A. | AB=CD | B. | 当AC⊥BD时,它是菱形 | ||
| C. | AB=AC | D. | 当∠ABC=90°时,它是矩形 |
分析 根据平行四边形的性质:对边平行且相等,对角线互相平分,可知A、B、D正确,无法得出AB=AC.
解答 解:A、平行四边形对边相等,故A正确;
B、对角线相互垂直的平行四边形是菱形,故正确;
C、无法得到AB=AC,故此选项错误,符合题意;
D、有一个角是90°的平行四边形是矩形.故正确.
故选:C.
点评 此题主要考查了平行四边形状中的特殊平行四边形的性质.要求熟记这些性质.如菱形中的对角线互相垂直平分和四边相等.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
6.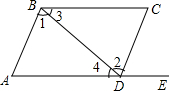 如图,给出下列条件:
如图,给出下列条件:
①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.
其中,能推出AB∥DC的条件为( )
 如图,给出下列条件:
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.
其中,能推出AB∥DC的条件为( )
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
13.等腰三角形的一边为3,另一边为6,则这个三角形的周长为( )
| A. | 15 | B. | 12或15 | C. | 9 | D. | 12 |
10.如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长为$\frac{1}{2}$的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(使其边长为前一块被剪掉正三角形纸板边长的$\frac{1}{2}$)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1的值( )
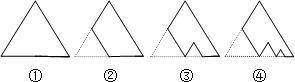

| A. | ${({\frac{1}{4}})^n}$ | B. | ${({\frac{1}{4}})^{n-1}}$ | C. | ${({\frac{1}{2}})^n}$ | D. | ${({\frac{1}{2}})^{n-1}}$ |
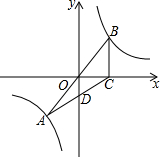 如图,A、B是反比例函数y=$\frac{k}{x}$图象上关于原点O对称的两点,BC⊥x轴,垂足为C,连线AC过点D(0,-1.5).若△ABC的面积为7,则点B的坐标为($\frac{7}{3}$,3).
如图,A、B是反比例函数y=$\frac{k}{x}$图象上关于原点O对称的两点,BC⊥x轴,垂足为C,连线AC过点D(0,-1.5).若△ABC的面积为7,则点B的坐标为($\frac{7}{3}$,3).