题目内容
16.甲、乙两人共同解方程组$\left\{\begin{array}{l}{ax+5y=15①}\\{4x-by=-2②}\end{array}\right.$,由于甲看错了方程①中的a,得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$;乙看错了方程②中的b,得到方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$.试计算a2006+(-$\frac{1}{10}$b)2007的值.分析 根据方程组的解的定义,解$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$应满足方程②,解$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$应满足方程①,将它们分别代入方程②①,就可得到关于a,b的二元一次方程组,解得a,b的值,代入代数式即可.
解答 解:甲看错了①式中x的系数a,解得$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,但满足②式的解,所以-12+b=-2,解得b=10;
同理乙看错了②式中y的系数b,解$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$,满足①式的解,所以5a+20=15,解得a=-1.
把a=-1,b=10代入a2006+(-$\frac{1}{10}$b)2007=1-1=0
点评 此题主要考查了二元一次方程组解的定义,以及解二元一次方程组的基本方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.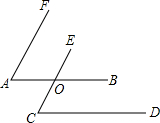 如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
 如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )| A. | 30° | B. | 60° | C. | 80° | D. | 120° |
1.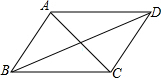 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )| A. | AB=CD | B. | 当AC⊥BD时,它是菱形 | ||
| C. | AB=AC | D. | 当∠ABC=90°时,它是矩形 |
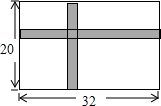 校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2,小道的宽应是2米.
校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2,小道的宽应是2米. 如图,已知△ABC.
如图,已知△ABC. 如图,正方形ABCD的边长为a,面积为6;正方形CEFG的边长为b,面积为2.求△BDF的面积.
如图,正方形ABCD的边长为a,面积为6;正方形CEFG的边长为b,面积为2.求△BDF的面积. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. 如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD.若∠EAO=15°,求∠BOE的度数.
如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD.若∠EAO=15°,求∠BOE的度数.