题目内容
10.如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长为$\frac{1}{2}$的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(使其边长为前一块被剪掉正三角形纸板边长的$\frac{1}{2}$)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1的值( )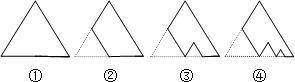
| A. | ${({\frac{1}{4}})^n}$ | B. | ${({\frac{1}{4}})^{n-1}}$ | C. | ${({\frac{1}{2}})^n}$ | D. | ${({\frac{1}{2}})^{n-1}}$ |
分析 利用等边三角形的性质(三边相等)求出等边三角形的周长P1,P2,P3,P4,根据周长相减的结果能找到规律即可求出答案.
解答 解:∵P1=1+1+1=3,
P2=1+1+$\frac{1}{2}$=$\frac{5}{2}$,
P3=1+1+$\frac{1}{4}$×3=$\frac{11}{4}$,
P4=1+1+$\frac{1}{4}$×2+$\frac{1}{8}$×3=$\frac{23}{8}$,
…
∴p3-p2=$\frac{11}{4}$-$\frac{5}{2}$=$\frac{1}{4}$=($\frac{1}{2}$)2;
P4-P3=$\frac{23}{8}$-$\frac{11}{4}$=$\frac{1}{8}$=($\frac{1}{2}$)3,
…
则Pn-Pn-1=($\frac{1}{2}$)n-1.
故选:D.
点评 此题考查图形的变化规律,通过观察图形,分析、归纳发现其中的运算规律,并应用规律解决问题.

练习册系列答案
相关题目
1.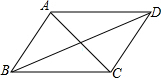 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )| A. | AB=CD | B. | 当AC⊥BD时,它是菱形 | ||
| C. | AB=AC | D. | 当∠ABC=90°时,它是矩形 |
15.若y轴上的点A到x轴的距离为3,则点A的坐标为( )
| A. | (3,0) | B. | (3,0)或(-3,0) | C. | (0,3) | D. | (0,3)或(0,-3) |
2. 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
20.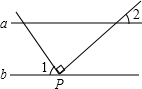 如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )
如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )
 如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )
如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )| A. | 24° | B. | 34° | C. | 44° | D. | 54° |
 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.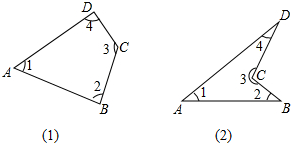 求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.