题目内容
9.计算(1)$\frac{1}{4}$x3y2•(-2xy2)
(2)($\frac{3}{4}$ab2-6ab)•(-$\frac{8}{3}$ab)
(3)(2x-3)2-(3x-1)(x+2)
(4)[($\frac{1}{2}$a-b)2+($\frac{1}{2}$a+b)2]($\frac{1}{2}$a2-2b2)
分析 (1)利用同底数幂的乘法计算;
(2)按照多项式乘单项式的计算方法计算;
(3)利用完全平方公式和整式的乘法计算即可;
(4)利用完全平方公式和平方差公式计算即可.
解答 解:(1)原式=-$\frac{1}{2}$x4y4;
(2)原式=-2a2b3+16a2b2;
(3)原式=4x2-12x+9-3x2-5x+2
=x2-17x+11;
(4)原式=[$\frac{1}{4}$a2-ab+b2+$\frac{1}{4}$a2+ab+b2]($\frac{1}{2}$a2-2b2)
=($\frac{1}{2}$a2-2b2)($\frac{1}{2}$a2-2b2)
=$\frac{1}{4}$a4-4b4.
点评 此题考查整式的混合运算,掌握计算是方法和运算顺序是正确计算的前提.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.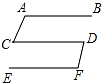 如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
 如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )
如图,AB∥CD∥EF,AC∥DF,若∠BAC=150°,则∠CDF=( )| A. | 30° | B. | 60° | C. | 150° | D. | 150° |
17.a<b,则下列不等式一定成立的是( )
| A. | a2<b2 | B. | ac2<bc2 | C. | ac<bc | D. | a-b<0 |
14.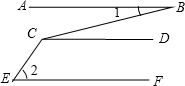 如图,若AB∥CD,CD∥EF,那么∠BCE=( )
如图,若AB∥CD,CD∥EF,那么∠BCE=( )
 如图,若AB∥CD,CD∥EF,那么∠BCE=( )
如图,若AB∥CD,CD∥EF,那么∠BCE=( )| A. | ∠1+∠2 | B. | 180°-∠1+∠2 | C. | ∠2-∠1 | D. | 180°-∠2+∠1 |
1.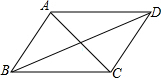 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )| A. | AB=CD | B. | 当AC⊥BD时,它是菱形 | ||
| C. | AB=AC | D. | 当∠ABC=90°时,它是矩形 |
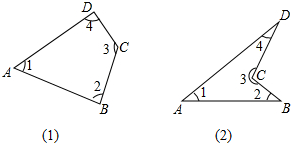 求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.