题目内容
8.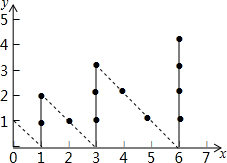 如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )
如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )| A. | 45 | B. | 946 | C. | 990 | D. | 1035 |
分析 设当横坐标为n时,实心点最多运动的次数为an,考虑多点横坐标相同的情况,观察图形可知这些点的横坐标分别为:1、1+2、1+2+3、…,数出最多运动的次数,根据数据的变化即可得出${a}_{\frac{n(n+1)}{2}}$=(n+1)2,解(n+1)2≤2017可得出n≤43,找出当n=43、44时,横坐标的值以及an的值,将其与2017进行比较即可得出结论.
解答 解:设当横坐标为n时,实心点最多运动的次数为an,
观察图形,可知:a1=4,a3=9,a6=16,
∵1=1,3=1+2,6=1+2+3,
∴${a}_{\frac{n(n+1)}{2}}$=(n+1)2.
令(n+1)2≤2017,
解得:n≤43.
当n=43时,$\frac{n(n+1)}{2}$=946,a946=1936,
当n=44时,$\frac{n(n+1)}{2}$=990,a990=2025.
∵1936+990-946-1=1979,
1979<2017<2025,
∴运动到第2017次时实心点所在位置的横坐标为990.
故选C.
点评 本题考查了规律型中点的坐标,观察图形结合实心点的运动,找出“${a}_{\frac{n(n+1)}{2}}$=(n+1)2”是解题的关键.

练习册系列答案
相关题目
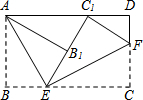
19. 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )| A. | ∠A=∠D | B. | ∠ACB=∠DFE | C. | AC=DF | D. | BE=CF |
16. 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )| A. | 6 cm2 | B. | 8 cm2 | C. | 10 cm2 | D. | 12 cm2 |
20.下列调查的样本选取方式,最具有代表性的是( )
| A. | 在青少年中调查年度最受欢迎的男歌手 | |
| B. | 了解班上学生的睡眠时间.调查班上学号为双号的学生的睡眠时间 | |
| C. | 为了了解你所在学校的学生每天的上网时间,向八年级的同学进行调查 | |
| D. | 对某市的出租司机进行体检,以此反映该市市民的健康状况 |
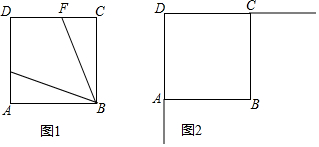
17. 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
18.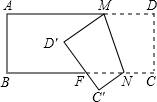 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |