题目内容
18．
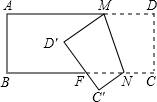如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=35°，则∠NFD′等于（ ）| A． | 115° | B． | 125° | C． | 135° | D． | 145° |
分析 根据∠AMD′=35°和折叠的性质，得∠NMD=∠NMD′=72.5°；根据平行线的性质，得∠BNM=∠NMD=72.5°；根据折叠的性质，得∠D′=∠D=90°；根据四边形的内角和定理即可求得∠NFD′的值．
解答 解：∵∠AMD′=35°，
∴∠NMD=∠NMD′=72.5°．
∵AD∥BC，
∴∠BNM=∠NMD=72.5°．
又∵∠D′=∠D=90°，
∴∠NFD′=360°-72.5°×2-90°=125°．
故选B．
点评 此题考查的是平行线的性质，综合运用了折叠的性质、四边形的内角和定理等知识，难度适中．
练习册系列答案
相关题目
8．
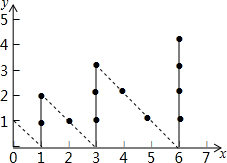如图，一个实心点从原点出发，沿下列路径（0，0）→（0，1）→（1，0）→（1，1）→（1，2）→…每次运动一个点，则运动到第2017次时实心点所在位置的横坐标为（ ）
如图，一个实心点从原点出发，沿下列路径（0，0）→（0，1）→（1，0）→（1，1）→（1，2）→…每次运动一个点，则运动到第2017次时实心点所在位置的横坐标为（ ）| A． | 45 | B． | 946 | C． | 990 | D． | 1035 |
9．若64x2+axy+y2是一个完全平方式，那么a的值应该是（ ）
| A． | 8 | B． | 16 | C． | -16 | D． | 16或-16 |
6．
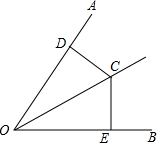如图，OC是∠AOB的角平分线．D，E分别是OA，OB上的点，则下列条件中不能判定△OCD与△OCE全等的是（ ）
如图，OC是∠AOB的角平分线．D，E分别是OA，OB上的点，则下列条件中不能判定△OCD与△OCE全等的是（ ）| A． | ∠OCD=∠OCE | B． | CD⊥OA，CE⊥OB | C． | OD=OE | D． | CD=CE |
13．若2m=3，2n=4，则23m-2n等于（ ）
| A． | $\frac{27}{16}$ | B． | $\frac{27}{8}$ | C． | $\frac{9}{8}$ | D． | 11 |
10．在函数y=$\frac{\sqrt{3x+6}}{x}$中，自变量x的取值范围是（ ）
| A． | x≥-2 | B． | x＞-0 | C． | x≥-2且x≠0 | D． | x＞-2且x≠0 |
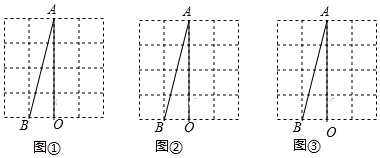
7．
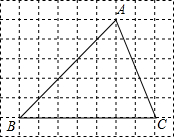在正方形网格中，△ABC的位置如图所示，则cos∠B的值为（ ）
在正方形网格中，△ABC的位置如图所示，则cos∠B的值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 1 |
8．下列运算正确的是（ ）
| A． | 3a+2a2=5a2 | B． | （ab）2=ab2 | C． | a•a=a2 | D． | 2（a+b）=2a+b |