题目内容
3.在正方形ABCD中,E、F分别为射线DA、DC上的点(与正方形顶点不重合),AE=CF,作GF=BF交射线AB于点G,直线GF与BE交于点H.(1)若点E、F分别在边DA、DC上,如图1,
①依题意补全图1;
②判断BE与GF的位置关系,并加以证明;
(2)若E、F分别在边DA、DC的延长线上,用等式表示线段EH、FH、DH之间的数量关系,并写出你的证明思路.
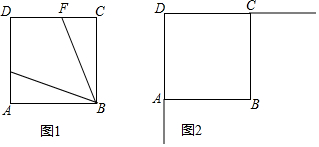
分析 (1)①画出图形;
②如图2,作辅助线,构建全等三角形,证明△ABE≌△BCF和Rt△EAB≌Rt△MBC,得∠MCB=∠ABE,则∠MNB=90°,所以GF⊥BE;
(2)作辅助线,构建全等三角形和等腰直角三角形,证明△AEB≌△MFG和△DEN≌△DFH,得DN=DH,∠NDE=∠HDF,再证明△NDH是等腰直角三角形,可得结论.
解答 解:(1)①如图1所示:
②BE⊥GF,理由是:
如图2,过C作CM∥GF,交AB于M,交BE于N,
∵四边形ABCD为正方形,
∴DC∥AB,AB=CB,∠A=∠DCB=90°,
∴FC∥GM,
∴四边形FGMC为平行四边形,
∴CM=GF,
∵GF=BF,
∴CM=BF,
∵AE=CF,∠A=∠DCB,AB=BC,
∴△ABE≌△BCF(SAS),
∴BE=BF,
∴CM=BE,
∴Rt△EAB≌Rt△MBC(HL),
∴∠MCB=∠ABE,
∵∠MCB+∠CMB=90°,
∴∠CMB+∠ABE=90°,
∴∠MNB=90°,
∵GF∥CM,
∴∠GHB=∠MNB=90°,
∴GF⊥BE;
(2)FH+EH=$\sqrt{2}$DH,理由是:
如图3,由(2)得:BE=BF=GF,
过G作GM⊥DC于M,
同理得:△AEB≌△MFG,
∴∠AEB=∠GFM,
延长BE至N,使FH=EN,连接DN,
∵AD=DC,AE=CF,
∴AD+AE=DC+CF,
即AE=DF,
∵∠AEB=∠GFM,
∴∠DEN=∠DFH,
∴△DEN≌△DFH(SAS),
∴DN=DH,∠NDE=∠HDF,
∵∠EDF=90°,
∴∠NDH=90°,
∴△NDH是等腰直角三角形,
∴NH=$\sqrt{2}$DH,
即NE+EH=$\sqrt{2}$DH,
∴FH+EH=$\sqrt{2}$DH.
点评 本题是四边形的综合题,考查了正方形的性质、全等三角形的性质和判定、等腰直角三角形的性质和判定,第3问作辅助线构建等腰直角△DNH是关键,本题难度适中.

| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
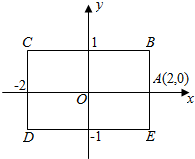 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )| A. | (2,0) | B. | (-1,1) | C. | (-2,1) | D. | (-1,-1) |
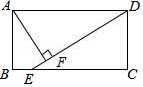 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )| A. | AF=$\frac{1}{2}$AD | B. | AB=AF | C. | △AFD≌△DCE | D. | BE=AD-DF |
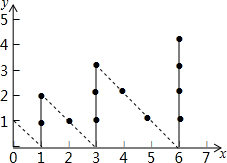 如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )
如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )| A. | 45 | B. | 946 | C. | 990 | D. | 1035 |
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)直角三角形两锐角互余;
(4)相等的角是对顶角.
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
| A. | a≥1 | B. | a>1 | C. | a=1 | D. | a≤1 |
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{9}{8}$ | D. | 11 |
 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )


