题目内容
17.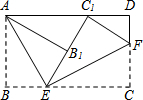 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
分析 根据直角三角形30°角所对的直角边等于斜边的一半求出AE=2,再根据直角三角形两锐角互余求出∠AEB=60°,根据翻折变换的性质可得∠AEB1=∠AEB,根据两直线平行,内错角相等可得∠EAC1=∠AEB1=60°,然后判断出△AEC1是等边三角形,根据等边三角形的性质可得BC1=AE,再根据翻折变换的性质可得EC=BC1.
解答 解:∵矩形纸片ABCD,∠BAE=30°,
∴AE=2BE=2×1=2,
∠AEB=90°-∠BAE=90°-30°=60°,
∵AB沿AE翻折点B落在EC1边上的B1处,
∴∠AEB1=∠AEB=60°,
∵矩形对边AD∥BC,
∴∠EAC1=∠AEB1=60°,
∴△AEC1是等边三角形,
∴BC1=AE=2,
∵EC沿BF翻折点C落在AD边上的C1处,
∴EC=BC1=2.
故选B.
点评 本题考查了翻折变换,直角三角形30°角所对的直角边等于斜边的一半,等边三角形的判定与性质,熟记翻折前后对应边相等,对应角相等是解题的关键.

练习册系列答案
相关题目
7.点P1(x1,y1)、P2(x2,y2)是一次函数y=-4x+3图象上的两点,当x1<x2<0时,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1<y2<0 | D. | y1>y2>0 |
8.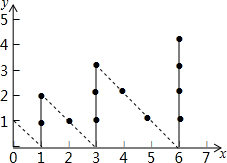 如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )
如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )
 如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )
如图,一个实心点从原点出发,沿下列路径(0,0)→(0,1)→(1,0)→(1,1)→(1,2)→…每次运动一个点,则运动到第2017次时实心点所在位置的横坐标为( )| A. | 45 | B. | 946 | C. | 990 | D. | 1035 |
5.下列分解因式正确的是( )
| A. | -ma-m=-m(a-1) | B. | a2-1=(a-1)2 | C. | a2-6a+9=(a-3)2 | D. | a2+2a+4=(a+2)2 |
12.如果式子$\sqrt{a-1}$是二次根式,那么a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a=1 | D. | a≤1 |
2.把点A(2,-3)先向上平移2个单位,再向左平移3个单位得到的点的坐标为( )
| A. | (4,0) | B. | (-1,-1) | C. | (5,-1) | D. | (-1,-5) |
9.若64x2+axy+y2是一个完全平方式,那么a的值应该是( )
| A. | 8 | B. | 16 | C. | -16 | D. | 16或-16 |
6.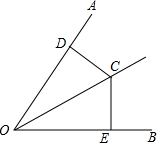 如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
 如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )| A. | ∠OCD=∠OCE | B. | CD⊥OA,CE⊥OB | C. | OD=OE | D. | CD=CE |
7.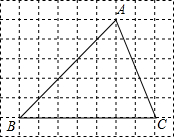 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |