题目内容
16.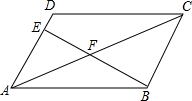 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )| A. | 2:3 | B. | 4:9 | C. | 6:11 | D. | 6:13 |
分析 由四边形ABCD是平行四边形,得到AD∥BC,AD=BC,根据相似三角形的性质得到$\frac{AE}{BC}=\frac{AF}{CF}=\frac{EF}{BF}$=$\frac{2}{3}$,求得S△BCF=$\frac{3}{2}$S1,S2=$\frac{3}{2}$S1,即可得到结论.
解答 解:∵在平行四边形ABCD中,AE:AD=2:3,
∴$\frac{AE}{AD}=\frac{2}{3}$,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△AEF∽△BCF,
∴$\frac{AE}{BC}=\frac{AF}{CF}=\frac{EF}{BF}$=$\frac{2}{3}$,
∴S△BCF=$\frac{3}{2}$S1
∴S四边形ABCD=2(S1+$\frac{3}{2}$S1)=5S1,
S△AEF=$\frac{2}{3}$S1,
∴S2=$\frac{1}{2}$S四边形ABCD-S△AEF=$\frac{11}{6}$S1,
∴S1:S2=$\frac{6}{11}$.
故选C.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,三角形的面积的计算,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
4.若a>b,则下列不等式中,不成立的是( )
| A. | a-3>b-3 | B. | -3a>-3b | C. | $\frac{a}{3}$>$\frac{b}{3}$ | D. | a+3>b+3 |
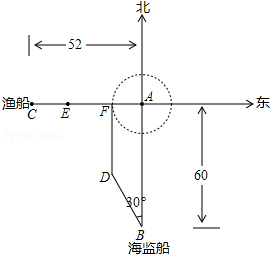 钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓 鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.
钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓 鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.