题目内容
6.解方程(1)7(2y-1)-3(4y-1)-5(3y+2)+1=0;
(2)$\frac{x+2}{4}$-$\frac{2x-3}{6}$=1.
分析 (1)先去括号,再移项,合并同类项,y的系数化为1即可;
(2)先去分母,再去括号,再移项,合并同类项,把x的系数化为1即可.
解答 解:(1)去括号得,14y-7-12y+3-15y-10+1=0
移项得,14y-12y-15y=7-3+10-1,
合并同类项得,-13y=13,
y的系数化为1得,y=-1;
(2)去分母得,3(x+2)-2(2x-3)=12,
去括号得,3x+6-4x+6=12,
移项得,3x-4x=12-6-6,
合并同类项得,-x=0,
把x的系数化为1得,x=0
点评 本题考查的是解一元一次方程,解一元一次方程时先观察方程的形式和特点,若有分母一般先去分母;若既有分母又有括号,且括号外的项在乘括号内各项后能消去分母,就先去括号.

练习册系列答案
相关题目
14.方程|x-3|=6的解是( )
| A. | 9 | B. | ±9 | C. | 3 | D. | 9或-3 |
11.方程-2x+3=0的解是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
18.代数式x2-kx$+\frac{25}{4}$是一个完全平方式,则k的取值为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | $±\frac{5}{2}$ | D. | ±5 |
15.下列能构成直角三角形的一组数是( )
| A. | 2、3、4 | B. | 6、8、9 | C. | 5、12、13 | D. | 1、1、2 |
16.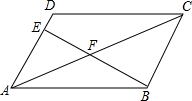 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )| A. | 2:3 | B. | 4:9 | C. | 6:11 | D. | 6:13 |
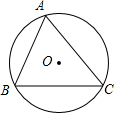 如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.
如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.