题目内容
13.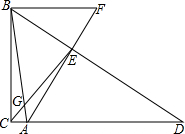 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.(1)当点E是BD的中点时,求tan∠AFB的值;
(2)CE•AF的值是否随线段AD长度的改变而变化?如果不变,求出CE•AF的值;如果变化,请说明理由;
(3)当△BGE和△BAF相似时,求线段AF的长.
分析 (1)过点E作EH⊥CD于H,如图1,易证EH是△DBC的中位线及△AHE∽△EHD,设AH=x,运用相似三角形的性质可求出x,就可求出tan∠AFB的值;
(2)取AB的中点O,连接OC、OE,如图2,易证四点A、C、B、E共圆,根据圆周角定理可得∠BCE=∠BAF,根据圆内接四边形内角互补可得∠CBE+∠CAE=180°,由此可推出∠CBE=∠BFA,从而可得△BCE∽△FAB,即可得到CE•FA=BC•AB,只需求出AB就可解决问题;
(3)过点E作EH⊥CD于H,作EM⊥BC于M,如图3,易证四边形EMCH是矩形,由△BCE∽△FAB,△BGE与△FAB相似可得△BGE与△BCE相似,即可得到∠EBG=∠ECB.由点A、C、B、E共圆可得∠ECA=∠EBG,即可得到∠ECB=∠ECA,根据角平分线的性质可得EM=EH,即可得到矩形EMCH是正方形,则有CM=CH,易证EB=EA,根据HL可得Rt△BME∽Rt△AHE,则有BM=AH.设AH=x,根据CM=CH可求出x,由此可求出CE的长,再利用(2)中的结果就可求出AF的值.
解答 解:(1)过点E作EH⊥CD于H,如图1,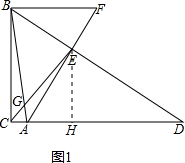
则有∠EHA=∠EHD=90°.
∵∠BCD=90°,BE=DE,
∴CE=DE.
∴CH=DH,
∴EH=$\frac{1}{2}$BC=$\frac{7}{2}$.
设AH=x,则DH=CH=x+1.
∵AE⊥BD,
∴∠AEH+∠DEH=∠AED=90°.
∵∠AEH+∠EAH=90°,
∴∠EAH=∠DEH,
∴△AHE∽△EHD,
∴$\frac{AH}{EH}$=$\frac{EH}{DH}$,
∴EH2=AH•DH,
∴($\frac{7}{2}$)2=x(x+1),
解得x=$\frac{5\sqrt{2}-1}{2}$(舍负),
∴tan∠EAH=$\frac{EH}{AH}$=$\frac{\frac{7}{2}}{\frac{5\sqrt{2}-1}{2}}$=$\frac{5\sqrt{2}+1}{7}$.
∵BF∥CD,
∴∠AFB=∠EAH,
∴tan∠AFB=$\frac{5\sqrt{2}+1}{7}$;
(2)CE•AF的值不变.
取AB的中点O,连接OC、OE,如图2,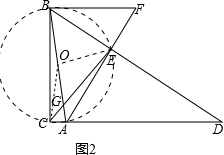
∵∠BCA=∠BEA=90°,
∴OC=OA=OB=OE,
∴点A、C、B、E共圆,
∴∠BCE=∠BAF,∠CBE+∠CAE=180°.
∵BF∥CD,
∴∠BFA+∠CAE=180°,
∴∠CBE=∠BFA,
∴△BCE∽△FAB,
∴$\frac{BC}{FA}$=$\frac{CE}{AB}$,
∴CE•FA=BC•AB.
∵∠BCA=90°,BC=7,AC=1,
∴AB=5$\sqrt{2}$,
∴CE•FA=7×5$\sqrt{2}$=35$\sqrt{2}$;
(3)过点E作EH⊥CD于H,作EM⊥BC于M,如图3,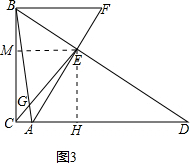
∴∠EMC=∠MCH=∠CHE=90°,
∴四边形EMCH是矩形.
∵△BCE∽△FAB,△BGE与△FAB相似,
∴△BGE与△BCE相似,
∴∠EBG=∠ECB.
∵点A、C、B、E共圆,
∴∠ECA=∠EBG,
∴∠ECB=∠ECA,
∴EM=EH,
∴矩形EMCH是正方形,
∴CM=CH.
∵∠ECB=∠ECA=$\frac{1}{2}$∠BCA=45°,
∴∠EBA=∠EAB=45°,
∴EB=EA,
∴Rt△BME≌Rt△AHE(HL),
∴BM=AH.
设AH=x,则BM=x,CM=7-x,CH=1+x,
∴7-x=1+x,
∴x=3,
∴CH=4.
在Rt△CHE中,
cos∠ECH=$\frac{CH}{CE}$=$\frac{4}{CE}$=$\frac{\sqrt{2}}{2}$,
∴CE=4$\sqrt{2}$.
由(2)可得CE•FA=35$\sqrt{2}$,
∴AF=$\frac{35\sqrt{2}}{4\sqrt{2}}$=$\frac{35}{4}$.
点评 本题主要考查了直角三角形斜边上的中线等于斜边的一半、等腰三角形的性质、三角形中位线定理、平行线的性质、相似三角形的判定与性质、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值、正方形的判定与性质等知识,综合性强,有一定的难度,证到△BCE∽△FAB是解决第(2)小题的关键,证出Rt△BME≌Rt△AHE是解决第(3)小题的关键.

 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )| A. | $\frac{12}{25}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
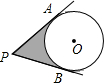 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
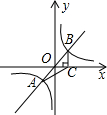 如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 10 |
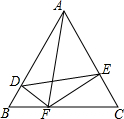 如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.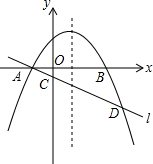 如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a<0)与x轴交于A、B两点,点A的坐标为(-2,0),经过点A的直线与y轴负半轴交于点C,与抛物线的另个一交点为D,且CD=3AC.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a<0)与x轴交于A、B两点,点A的坐标为(-2,0),经过点A的直线与y轴负半轴交于点C,与抛物线的另个一交点为D,且CD=3AC.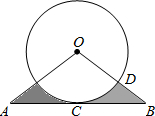 如图,线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=3cm,AB=3$\sqrt{3}$cm,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}-\frac{3}{4}π$.
如图,线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=3cm,AB=3$\sqrt{3}$cm,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}-\frac{3}{4}π$.