题目内容
2.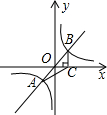 如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 10 |
分析 由题意得:S△ABC=2S△AOC,又S△AOC=$\frac{1}{2}$|k|,则k的值即可求出.
解答 解:设A(x,y),
∵直线与双曲线y=$\frac{k}{x}$交于A、B两点,
∴B(-x,-y),
∴S△BOC=$\frac{1}{2}$|xy|,S△AOC=$\frac{1}{2}$|xy|,
∴S△BOC=S△AOC,
∴S△ABC=S△AOC+S△BOC=2S△AOC=5,S△AOC=$\frac{1}{2}$|k|=$\frac{5}{2}$,则k=±5.
又由于反比例函数位于一三象限,k>0,故k=5.
故选C.
点评 本题主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.

练习册系列答案
相关题目
12. 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )
 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠4 | D. | ∠5=∠1+∠3 |
17.2015年末青岛市常住人口数约为9050000人,将9050000用科学记数法表示为( )
| A. | 9.05×106 | B. | 0.905×106 | C. | 0.905×107 | D. | 9.05×107 |
12.在平行四边形、菱形、矩形、正方形、等边三角形这五种图形中,既是轴对称图形,又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
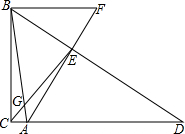 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.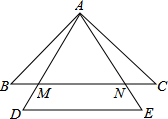 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN. 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹.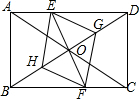 已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.