题目内容
5.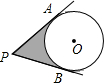 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
分析 如果连接OA、OB、OP,那么阴影部分的面积可以用两个直角三角形的面积和圆心角为120°的扇形的面积差来求得.
解答 解:连接OA,OB,OP,则∠OAP=∠OBP=90°,
∴∠AOB=180°-60°=120°,∠AOP=∠BOP=60°;
由切线长定理知,AP=PB=AOtan60°=3$\sqrt{3}$,
∴S阴影=S△APO+S△OPB-S扇形OAB;
即:S阴影=2×$\frac{1}{2}$×OA•AP-$\frac{120π×{3}^{2}}{360}$=9$\sqrt{3}$-3π.
故选A.
点评 本题考查了切线长定理以及直角三角形、扇形的面积的求法,关键是根据阴影部分的面积可以用两个直角三角形的面积和圆心角为120°的扇形的面积差解答.

练习册系列答案
相关题目
16.某课外兴趣小组为了了解所在地区老年人的健康状况,分别作了四种不同的抽样调查,你认为抽样比较合理的是( )
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 调查了10名老年人的健康状况 | |
| C. | 在医院调查了1000名老年人的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人健康状况 |
17.2015年末青岛市常住人口数约为9050000人,将9050000用科学记数法表示为( )
| A. | 9.05×106 | B. | 0.905×106 | C. | 0.905×107 | D. | 9.05×107 |
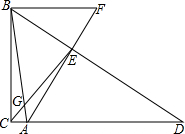 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.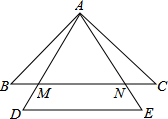 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.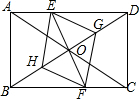 已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.