题目内容
1.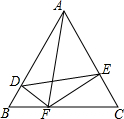 如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.(1)求证:△BDF∽△CEF;
(2)若a=4,试探究当BF取何值时,四边形ADFE的面积最大;
(3)已知tan∠EDF=$\frac{\sqrt{3}}{2}$,试证明四边形ADFE是圆内接四边形并求出此圆的直径.
分析 (1)只需找到两组对应角相等即可;
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,借助三角函数用m表示出AD、DF、AE、EF的长,进而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题;
(3)易知AF就是圆的直径,利用圆周角定理将∠EDF转化为∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通过解直角三角形就可求出AF长.
解答 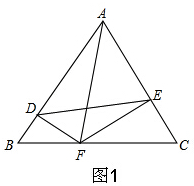 解:(1)∵DF⊥AB,EF⊥AC,
解:(1)∵DF⊥AB,EF⊥AC,
∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF;
(2)设BF=m,则DF=$\frac{\sqrt{3}}{2}$m,BD=$\frac{1}{2}$m,
∵AB=4,∴AD=4-$\frac{1}{2}$m,
∴S△ADF=$\frac{1}{2}$AD•DF=$\frac{1}{2}$(4-$\frac{1}{2}$m)×$\frac{\sqrt{3}}{2}$m=-$\frac{\sqrt{3}}{8}$m2+$\sqrt{3}$m,
同理:S△AEF=-$\frac{\sqrt{3}}{8}$m2+2$\sqrt{3}$,
∴S△DFE=S△ADF+S△AEF=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+2$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$(m-2)2+3$\sqrt{3}$,其中0<m<4.
∵-$\frac{\sqrt{3}}{4}$<0,0<2<4,
∴当m=2时,S△DEF取最大值,最大值为3$\sqrt{3}$,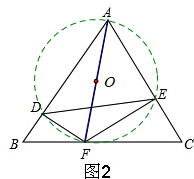
(3)设O是AF的中点,∵∠ADF=∠AEF=90°,∴OD=OE=$\frac{1}{2}$AF,
∴A、D、F、E到点O的距离相等,
即四边形ADFE是圆内接四边形,AF是此圆的直径,
∴∠EDF=∠EAF.
∵tan∠EDF=$\frac{\sqrt{3}}{2}$,∴tan∠EAF=$\frac{\sqrt{3}}{2}$.∴$\frac{EF}{EA}=\frac{\sqrt{3}}{2}$,
∵∠C=60°,∴$\frac{EF}{EC}$=tan60°=$\sqrt{3}$,
∴$\frac{EC}{EA}$=$\frac{1}{2}$,∴EC=$\frac{1}{3}$a,EA=$\frac{2}{3}$a,EF=$\frac{\sqrt{3}}{3}$a,
∴AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\frac{\sqrt{7}}{3}$a,
∴此圆直径长为$\frac{\sqrt{7}}{3}$a.
点评 本题考查了相似三角形的判定、二次函数的最值、三角函数、解直角三角形、圆周角定理、等边三角形的性质等知识,综合性强.利用圆周角定理将条件中的圆周角转化到合适的位置是解决最后一小题的关键.

 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠4 | D. | ∠5=∠1+∠3 |
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 调查了10名老年人的健康状况 | |
| C. | 在医院调查了1000名老年人的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人健康状况 |
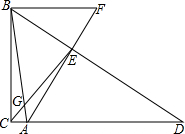 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.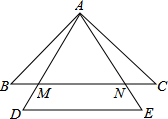 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.