题目内容
3.A和B两地相距140千米,甲、乙二人骑自行车分别从A和B两地同时出发,相向而行.丙驾驶摩托车,每小时行驶63千米,同时与甲从A出发,与乙相遇后立即返回,丙返回至甲时,甲、乙相距84千米.若甲车速是每小时9千米,则乙的速度为7千米/时.分析 可设丙驾驶摩托车与乙相遇时,甲行驶的路程是x千米,根据等量关系:甲、乙相距84千米,列出方程求解即可.
解答 解:设丙驾驶摩托车与乙相遇时,甲行驶的路程是x千米,依题意有
$\frac{7}{4}$x+$\frac{7}{4}$(140-7x)=140-84,
解得x=18,
$\frac{7}{4}$x=31.5,
$\frac{7}{4}$(140-7x)=$\frac{7}{4}$×(140-126)=24.5,
31.5÷9=3.5(小时),
24.5÷3.5=7(千米/时).
答:乙的速度为7千米/时.
故答案为:7.
点评 考查了一元一次方程的应用,根据速度比得到路程比是解题的关键,本题设出丙驾驶摩托车与乙相遇时,甲行驶的路程是x千米可以简化计算量.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
18.若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
| A. | 直线PQ可能与直线AB垂直 | |
| B. | 直线PQ可能与直线AB平行 | |
| C. | 过点P的直线一定能与直线AB相交 | |
| D. | 过点Q只能画出一条直线与直线AB平行 |
8.下列式子中与2ab2是同类项的是( )
| A. | 3ab | B. | 2b2 | C. | ab2 | D. | a2b |
12. 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )
 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠4 | D. | ∠5=∠1+∠3 |
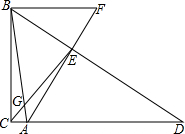 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.