题目内容
18. 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.(1)求c的值;
(2)将抛物线向下平移m个单位,使平移后的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围.
分析 (1)把点A的坐标代入函数解析式可以求得c的值;
(2)根据点A的坐标求得直线OA的解析式,然后求得对称轴x=-1与直线AB的交点坐标可以求得m的最小值,求得x=-1与直线OA的交点坐标可以求得m的最大值.
解答 解:(1)把点A的坐标是(-2,4)代入y=-x2-2x+c,得
4=-(-2)2-2×(-2)+c,
解得 c=4.
即c的值是4;
(2)由(1)得到抛物线的解析式为:y=-x2-2x+4=-(x+1)2+5,则该抛物线的顶点坐标是(-1,5).
∵点A的坐标是(-2,4),
∴当该抛物线向下平移1个单位时,抛物线的顶点在边AB上,故m>1.
易求直线OA的解析式为y=-2x.
把x=-1代入,得
y=2,
则抛物线向下平移3个单位后,顶点在边OA上,故m<3.
所以m的取值范围是1<m<3.
点评 本题考查了二次函数图象的几何变换.解题时需要注意题干中的限制性条件:平移后的抛物线顶点落在△OAB的内部,不包括△OAB的边界.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.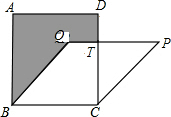 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )| A. | 23cm2 | B. | 33cm2 | C. | 43cm2 | D. | 53cm2 |
10.点E在正方形ABCD的边AB上,且BE=1cm,CE=2cm,则正方形的面积是( )
| A. | $\sqrt{3}$cm2 | B. | $\sqrt{5}$cm2 | C. | 3cm2 | D. | 5cm2 |