题目内容
8.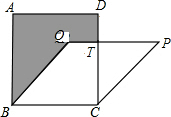 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )| A. | 23cm2 | B. | 33cm2 | C. | 43cm2 | D. | 53cm2 |
分析 先由正方形的面积求出边长,再由菱形的面积求出菱形的高,根据勾股定理求出PT和△CPT的面积,用整个图形的面积减去菱形的面积即为阴影部分的面积.
解答 解:∵正方形ABCD的面积为169cm2,
∴BC=$\sqrt{169}$=13,
又∵菱形BCPQ的面积为156cm2,
∴CT=$\frac{156}{13}$=12,CP=BC=13,
∴PT=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴△CPT的面积=$\frac{1}{2}$×12×5=30,
∴阴影部分的面积=正方形ABCD的面积+△CPT的面积-菱形BCPQ=169+30-156=43(cm2),
故选:C.
点评 本题考查了菱形的性质、正方形的性质以及勾股定理的运用;熟练掌握面积的计算方法是解决问题的关键.

练习册系列答案
相关题目
16.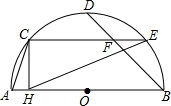 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
13.若ab=cd,且abcd≠0,则下列式子正确的是( )
| A. | a:c=b:d | B. | d:c=b:a | C. | a:b=c:d | D. | a:d=c:b |
20.如图是一个简单的数值运算程序,当输入的x的值为-1时,则输出的值为( )


| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
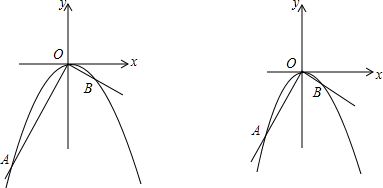
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.