题目内容
7.将(a+b)(c+d)展开后是4个单项式的和;将(a+b)(c+d+e)展开后是6个单项式的和;将(a+b+c)(d+e+f)展开后是9个单项式的和;…,以此类推,将(a1+a2+a3+…+am)(b1+b2+b3+…+bn)展开后是mn个单项式的和.
分析 观察可以发现4=2×2,6=2×3,9=3×3,即展开后单项式的个数=第一个多项式中单项式的个数×第二个多项式中单项式的个数,以次类推即可解答.
解答 解:∵(a+b)(c+d)展开后是4个单项式的和,4=2×2;
将(a+b)(c+d+e)展开后是6个单项式的和,6=2×3;
将(a+b+c)(d+e+f)展开后是9个单项式的和,9=3×3;
…,
即展开后单项式的个数=第一个多项式中单项式的个数×第二个多项式中单项式的个数,
以此类推,将(a1+a2+a3+…+am)(b1+b2+b3+…+bn)展开后是mn个单项式的和.
故答案为:mn.
点评 本题考查了多项式乘以多项式,解决本题的关键是分析问题,找到规律,即展开后单项式的个数=第一个多项式中单项式的个数×第二个多项式中单项式的个数.

练习册系列答案
相关题目
16.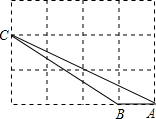 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
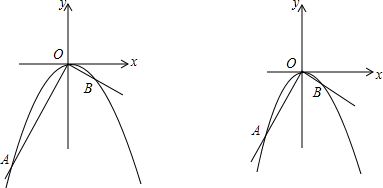
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.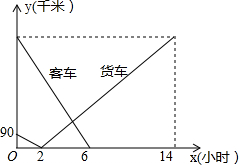 在一平直公路上依次有A、C、B三地,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车2小时可到达途中C站,14小时到达A地,客车需6小时到达C站.已知客车、货车到C站的距离与它们行驶时间x(小时)之间的函数关系如图所示,客车的速度比货车的速度快45千米/小时.
在一平直公路上依次有A、C、B三地,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车2小时可到达途中C站,14小时到达A地,客车需6小时到达C站.已知客车、货车到C站的距离与它们行驶时间x(小时)之间的函数关系如图所示,客车的速度比货车的速度快45千米/小时.