题目内容
6.解方程:(1)x2-2x=2x+1
(2)2x2+3x-1=0.
分析 (1)利用配方法得到(x-2)2=5,然后利用直接开平方法解方程;
(2)利用求根公式法解方程.
解答 解:(1)x2-4x=1,
x2-4x+4=5,
(x-2)2=5,
x-2=±$\sqrt{5}$,
所以x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(2)△=32-4×2×(-1)=17,
x=$\frac{-3±\sqrt{17}}{2×2}$
所以x1=$\frac{-3+\sqrt{17}}{4}$,x2=$\frac{-3-\sqrt{17}}{4}$.
点评 本题考查了解一元二次方程-公式法:把x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$(b2-4ac≥0)叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式,用求根公式解一元二次方程的方法是公式法.也考查了配方法解一元二次方程.

练习册系列答案
相关题目
16.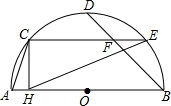 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
1.点A(3,-4)关于原点的对称点为( )
| A. | (3,4) | B. | (-3,4) | C. | (-3,-4) | D. | (4,3) |
16.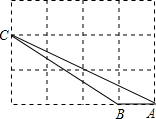 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
 如图,已知∠BOC=5∠AOC,OD平分∠AOB,且∠DOC=40°,求∠AOB的度数.
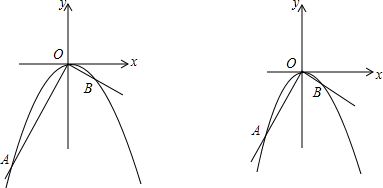
如图,已知∠BOC=5∠AOC,OD平分∠AOB,且∠DOC=40°,求∠AOB的度数. 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.