题目内容
13．三角形的两边分别为2和6，第三边是方程x2-10x+21=0的解，则第三边的长为7．分析 将已知的方程x2-10x+21=0左边分解因式，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程，求出一次方程的解得到原方程的解为3或7，利用三角形的两边之和大于第三边进行判断，得到满足题意的第三边的长
解答 解：x2-10x+21=0，
因式分解得：（x-3）（x-7）=0，
解得：x1=3，x2=7，
∵三角形的第三边是x2-10x+21=0的解，
∴三角形的第三边为3或7，
当三角形第三边为3时，2+3＜6，不能构成三角形，舍去；
当三角形第三边为7时，三角形三边分别为2，6，7，能构成三角形，
所以第三边的长为7．
故答案为7．
点评 此题考查了利用因式分解法求一元二次方程的解，以及三角形的边角关系，利用因式分解法解方程时，首先将方程右边化为0，左边分解因式，然后利用两数相乘积为0，两因式中至少有一个为0转化两个一次方程来求解
练习册系列答案
名校课堂系列答案
相关题目
1．点A（3，-4）关于原点的对称点为（ ）
| A． | （3，4） | B． | （-3，4） | C． | （-3，-4） | D． | （4，3） |
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA，若抛物线y=-x2-2x+c经过点A．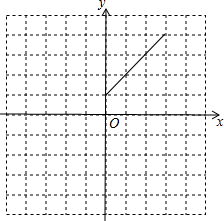
我们知道，把直线y=x向左平移1个单位可得到一次函数y=x+1的图象，把直线y=kx（k≠0）向左平移1个单位可得到一次函数y=k（x+1）的图象，把抛物线y=ax2（a≠0）向左平移1个单位，可得到二次函数y=a（x+1）2的图象．