题目内容
10．点E在正方形ABCD的边AB上，且BE=1cm，CE=2cm，则正方形的面积是（ ）| A． | $\sqrt{3}$cm2 | B． | $\sqrt{5}$cm2 | C． | 3cm2 | D． | 5cm2 |
分析 先根据勾股定理求出正方形的边长，再由正方形的面积=边长的平方，即可得出结果．
解答 
解：如图所示：∵四边形ABCD是正方形，
∴∠B=90°，
根据勾股定理得：BC=$\sqrt{C{E}^{2}-B{E}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴正方形的面积=（$\sqrt{3}$）2=3；
故选：C．
点评 本题考查了正方形的性质、勾股定理以及正方形面积的计算；运用勾股定理求出正方形的边长是解决问题的关键．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
20．如图是一个简单的数值运算程序，当输入的x的值为-1时，则输出的值为（ ）
| A． | -5 | B． | -1 | C． | 1 | D． | 5 |
1．点A（3，-4）关于原点的对称点为（ ）
| A． | （3，4） | B． | （-3，4） | C． | （-3，-4） | D． | （4，3） |
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA，若抛物线y=-x2-2x+c经过点A．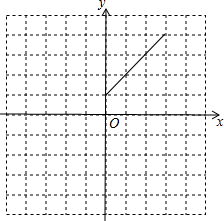
我们知道，把直线y=x向左平移1个单位可得到一次函数y=x+1的图象，把直线y=kx（k≠0）向左平移1个单位可得到一次函数y=k（x+1）的图象，把抛物线y=ax2（a≠0）向左平移1个单位，可得到二次函数y=a（x+1）2的图象．
如图所示，已知OB⊥OA，直线CD过点O，且∠AOC=35°，则∠BOD=125°．