题目内容
7.y=2x+b的图象经过第一、三、四象限,则b<0.分析 根据一次函数y=2x+b的图象经过第一、三、四象限求出b的取值范围即可.
解答 解:∵一次函数y=2x+b的图象经过第一、三、四象限,
∴b<0,
故答案为:<.
点评 本题考查的是一次函数的图象与系数的关系,一次函数y=kx+b(k≠0)中,当k>0,b<0时函数的图象在一、三、四象限.

练习册系列答案
相关题目
18.已知|a-6|+$\sqrt{b-8}$+(c-10)2=0,则这个三角形中最长的边上的高线为( )
| A. | 4 | B. | $\frac{24}{5}$ | C. | $\frac{40}{3}$ | D. | $\frac{15}{2}$ |
2.为了落实水资源管理制度,大力促进水资源节约,某地实行居民用水阶梯水价,收费标准如下表:
居民用水阶梯水价表 单位:元/立方米
(1)小明家5月份用水量为14立方米,在这个月,小明家需缴纳的水费为70元;
(2)小明家6月份缴纳水费110元,在这个月,小明家缴纳第二阶梯水价的用水量为5立方米;
(3)随着夏天的到来,用水量将会有所增加,为了节省开支,小明家计划7月份的水费不超过180元,在这个月,小明家最多能用水多少立方米?
居民用水阶梯水价表 单位:元/立方米
| 分档 | 户每月分档用水量x(立方米) | 水价 |
| 第一阶梯 | 0≤x≤15 | 5.00 |
| 第二阶梯 | 15<x≤21 | 7.00 |
| 第三阶梯 | x>21 | 9.00 |
(2)小明家6月份缴纳水费110元,在这个月,小明家缴纳第二阶梯水价的用水量为5立方米;
(3)随着夏天的到来,用水量将会有所增加,为了节省开支,小明家计划7月份的水费不超过180元,在这个月,小明家最多能用水多少立方米?
19.已知点(-2,y1),(-1,y2),(1,y3)都在直线y=-3x+2上,则y1,y2,y3的值的大小关系是( )
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y3>y1>y2 | D. | y1>y2>y3 |
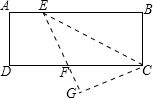 如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.
如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°. 如图,在平面直角坐标系xOy中,A,B,C,D四点的坐标分别是A(-2,3),B(4,3),C(0,1),D(1,2),动点P从点A出发,在线段AB上以每秒1个单位长度的速度向点B运动,到达点B时停止运动.射线PC,PD与x轴分别交于点M,点N,设点P运动的时间为t秒,若以点C,D,M,N为顶点能围成一个四边形,则t的取值范围是0≤t≤6且t≠4.
如图,在平面直角坐标系xOy中,A,B,C,D四点的坐标分别是A(-2,3),B(4,3),C(0,1),D(1,2),动点P从点A出发,在线段AB上以每秒1个单位长度的速度向点B运动,到达点B时停止运动.射线PC,PD与x轴分别交于点M,点N,设点P运动的时间为t秒,若以点C,D,M,N为顶点能围成一个四边形,则t的取值范围是0≤t≤6且t≠4. 如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是56°.
如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是56°.