题目内容
17.$\frac{2x}{{x}^{3}+2{x}^{2}+x}$÷$\frac{x-1}{{x}^{2}+x}$,其中x=-2.分析 首先化简$\frac{2x}{{x}^{3}+2{x}^{2}+x}$÷$\frac{x-1}{{x}^{2}+x}$,然后把x=-2代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{2x}{{x}^{3}+2{x}^{2}+x}$÷$\frac{x-1}{{x}^{2}+x}$
=$\frac{2}{{(x+1)}^{2}}$×$\frac{x(x+1)}{x-1}$
=$\frac{2x}{{x}^{2}-1}$
当x=-2时,
原式=$\frac{2×(-2)}{{(-2)}^{2}-1}$=-$\frac{4}{3}$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
相关题目

 如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.
如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.

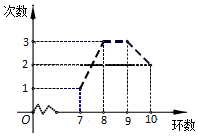 一名射击运动员连续打靶9次,假如他打靶命中环数的情况如图所示,那么该射击运动员本次打靶命中环数的中位数为9环.
一名射击运动员连续打靶9次,假如他打靶命中环数的情况如图所示,那么该射击运动员本次打靶命中环数的中位数为9环.